Transformaciones de Box-Cox

Thu, Aug 20, 2020 7-minute read

Para poder aplicar el método de los mínimos cuadrados ordinarios es necesario que se cumplan ciertos supuestos, particularmente los relacionados con los errores: su media debe ser cero, su varianza constante y deben ser independientes entre sí. Además, los errores deben ser independientes de las variables explicativas del modelo y, preferentemente, normales. Sin embargo, existen ocasiones en que estos supuestos no se satisfacen con nuestros datos disponibles. En estos casos, aun podemos aplicar alguna transformación que nos permita utilizar el método de los mínimos cuadrados ordinarios para estimar los coeficientes. Una de estas es la técnica de Box-Cox (1964).

Las transformaciones de Box-Cox son una familia de transformaciones potenciales usadas en estadística para corregir sesgos en la distribución de errores, para corregir varianzas desiguales y principalmente para corregir la no linealidad en la relación (mejorar correlación entre las variables). Específicamente, para una variable $y>0$ , el conjunto de transformaciones de Box-Cox es:

$y^{(\lambda)}=\frac{y^{\lambda}-1}{\lambda},$ donde $y^{(\lambda)}=\ln(y)$ en el límite $\lambda \rightarrow 0$ . Para otros valores de $\lambda$ tenemos, por ejemplo:

Modelo	$\lambda$	$y^{(\lambda)}$
Lineal	$1$	$y-1$
Raiz cuadrada	$0.5$	$2(\sqrt{y}-1)$
Logaritmo Natural	$0$	$\ln(y)$
Inversa	$-1$	$1-\frac{1}{y}$

Si elegimos el valor correcto de $\lambda$ obtenemos que la transformación de $y$ , $y^{\lambda}$ , está más cerca de ser simétrica.

Ejemplo

Para el siguiente ejemplo, utilizaremos los siguientes paquetes de R:

# Instalar paquetes si es necesario
# install.packages("tidyverse")
# install.packages("car")
# install.packages("moments")
# install.packages("MASS")

# Leer paquetes
library(tidyverse)

## ── Attaching packages ──────────────── tidyverse 1.3.0 ──

## ✓ ggplot2 3.3.2     ✓ purrr   0.3.4
## ✓ tibble  3.0.1     ✓ dplyr   1.0.0
## ✓ tidyr   1.1.0     ✓ stringr 1.4.0
## ✓ readr   1.3.1     ✓ forcats 0.5.0

## ── Conflicts ─────────────────── tidyverse_conflicts() ──
## x dplyr::filter() masks stats::filter()
## x dplyr::lag()    masks stats::lag()

library(car)

## Loading required package: carData

## 
## Attaching package: 'car'

## The following object is masked from 'package:dplyr':
## 
##     recode

## The following object is masked from 'package:purrr':
## 
##     some

library(moments)

## Warning: package 'moments' was built under R version 4.0.2

library(MASS)

## 
## Attaching package: 'MASS'

## The following object is masked from 'package:dplyr':
## 
##     select

Consideremos una muestra del Medical Expenditure Panel Survey 2004 de los Estados Unidos. Tómate un tiempo para analizar la base de datos, así como para realizar un análisis de estadística descriptiva.

db <- read_csv("https://raw.githubusercontent.com/amosino/courses--econometria/master/econometria_salud/econometria_salud--datos/MEPSData.csv")

## Parsed with column specification:
## cols(
##   .default = col_double(),
##   famidyr = col_character(),
##   hieuidx = col_character(),
##   female = col_character(),
##   race_bl = col_character(),
##   race_oth = col_character(),
##   eth_hisp = col_character(),
##   ed_hs = col_character(),
##   ed_hsplus = col_character(),
##   ed_col = col_character(),
##   reg_midw = col_character(),
##   reg_south = col_character(),
##   reg_west = col_character(),
##   anylim = col_character(),
##   ins_mcare = col_character(),
##   ins_mcaid = col_character(),
##   ins_unins = col_character(),
##   ins_dent = col_character()
## )

## See spec(...) for full column specifications.

Deseamos modelar la dependencia que existe entre los gastos totales en salud (exp_tot), los cuales juegan el papel de la variable dependiente, en función de la edad de la persona (age) y de su género (female). Esta es una variable dummy que vale Female si la observación es una mujer y Male si es hombre. Aunque R no tiene ningún problema manejando variables dummy cuyas características estén codificadas como texto, podemos recodificar, si así lo deseamos, la variable female, tal que esta valga 1 si la observación es una mujer y 0 si es hombre.

db$female <- as.factor(as.numeric(db$female=="Female"))

Estimamos el modelo por el método de los mínimos cuadrados ordinarios.

mod.lrm <- lm(exp_tot~age+female, data=db, subset=(exp_tot>0))
smod.lrm <- summary(mod.lrm)

Un histograma de los residuales del modelo nos revela que estos están sesgados hacia la izquierda.

hist(mod.lrm$residuals)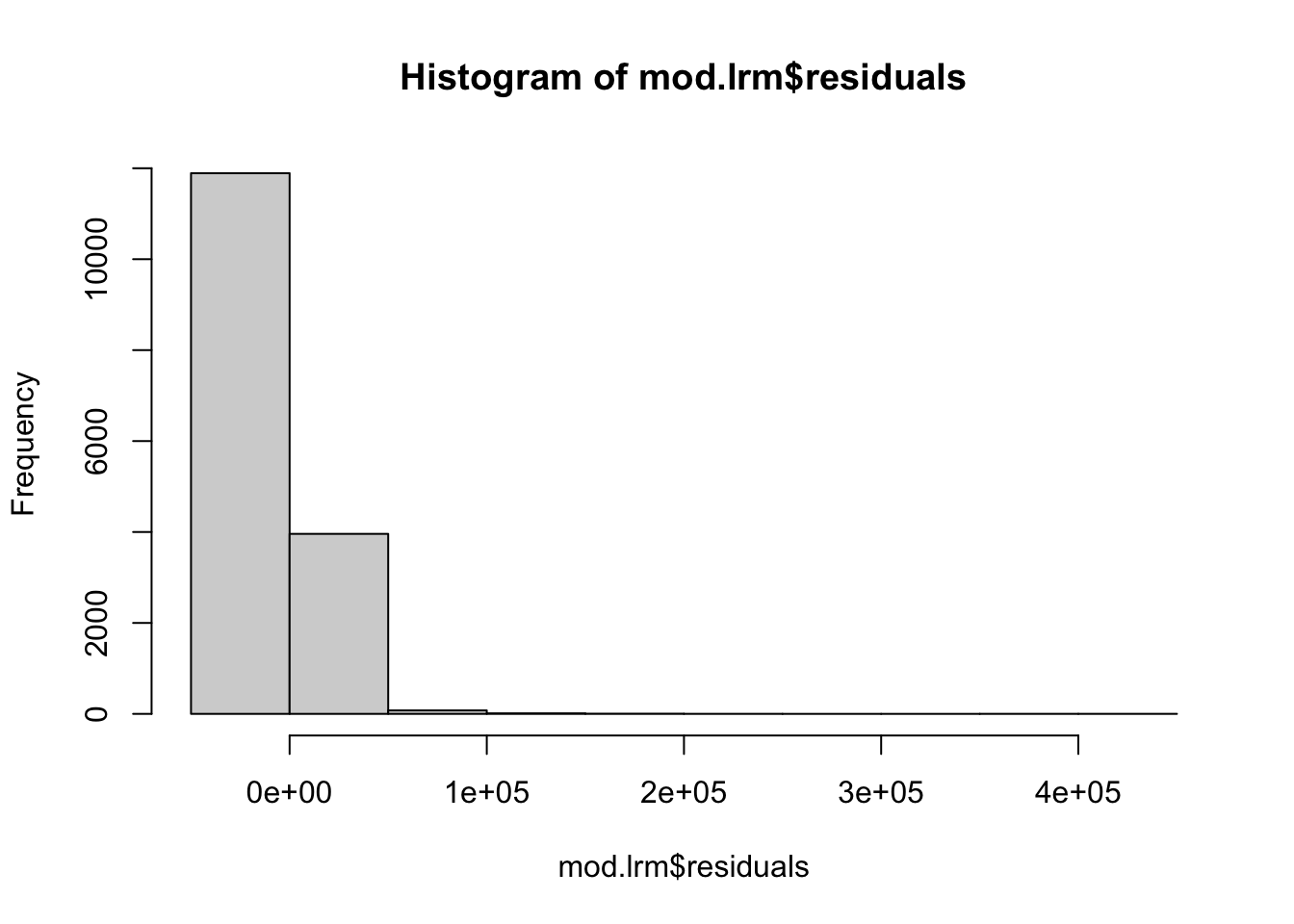

También podemos comparar los cuantiles de los residuales estandarizados contra los de una distribución normal. Estos son tan diferentes que es mu difícil confiar en que la distribución de los residuales es normal.

qqPlot(rstandard(mod.lrm))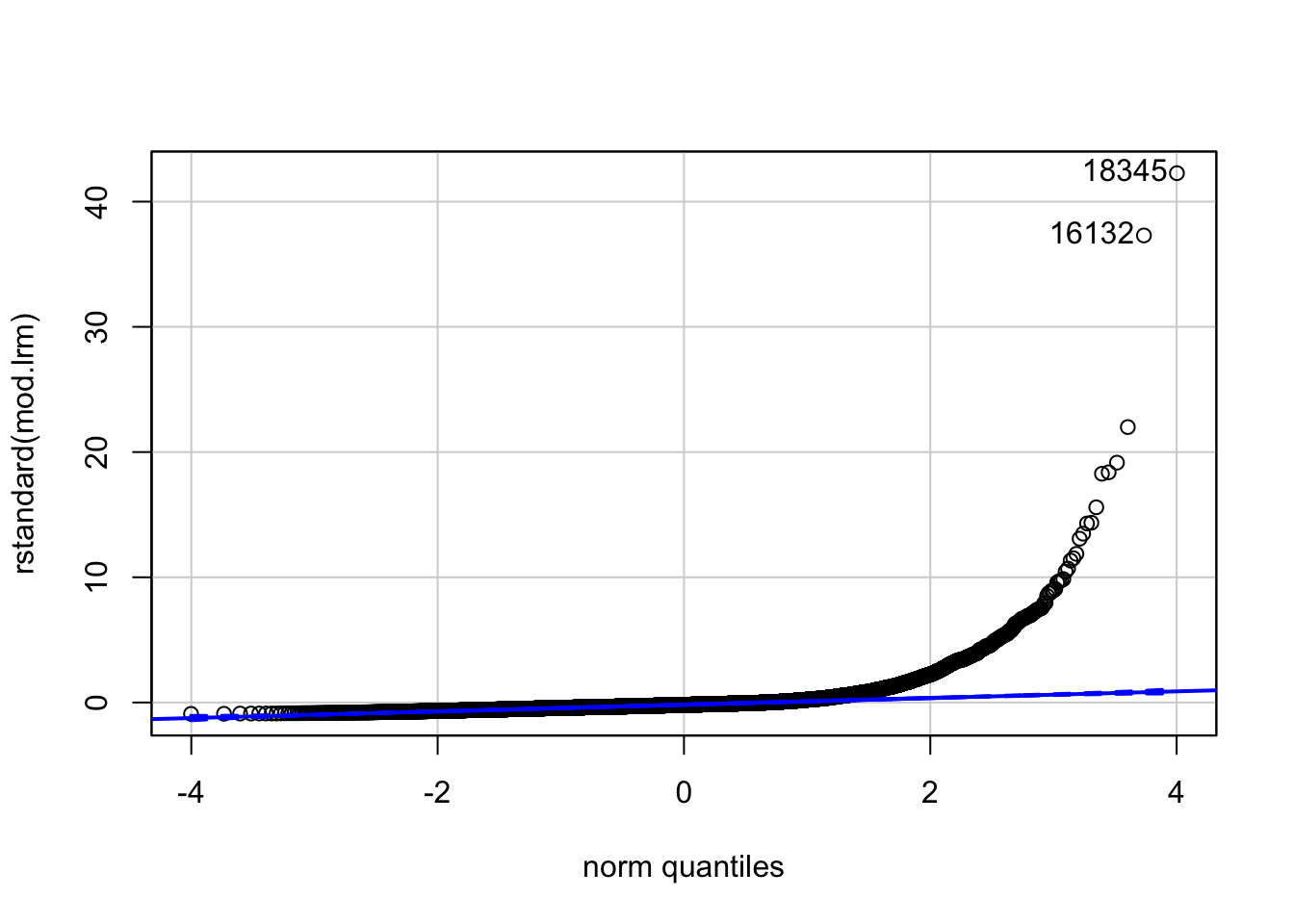

## 18345 16132 
## 15107 13326

Finalmente, podemos calcular los coeficientes de asimetría y curtósis de los residuales. Estos, como vemos, están muy lejos de los valores usuales para una distribición normal (aldededor de 0 y 3, respectivamente).

skewness(mod.lrm$residuals)

## [1] 13.50972

kurtosis(mod.lrm$residuals)

## [1] 390.7042

Busquemos ahora el valor de $\lambda$ que nos ayuda a tener una distribución de los residuales más simétrica. Primero, estimamos la función de máxima verosimilitud del modelo lineal. Una inspección visual de esta función nos indica que la mejor transformación para nuestro modelo es aquella en la cual $\lambda=0$ , es decir, una transformación logarítmica.

b <- boxcox(mod.lrm)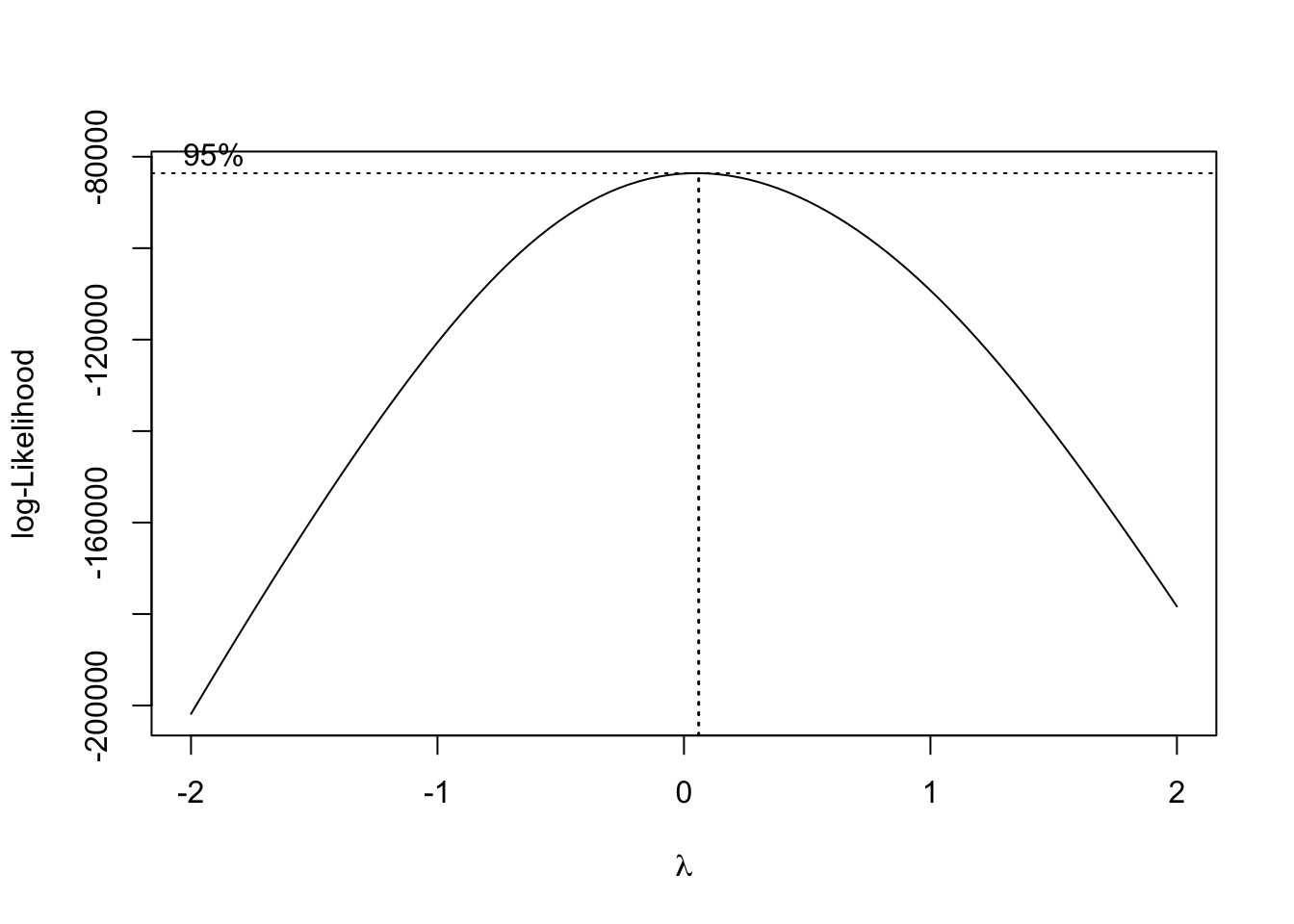

Lo anterior podemos corroborarlo extrayendo de la transformación de box-cox los valores numéricos de $\lambda$ y de la función de (log) verosimilitud.

lambda <- b$x
lik <- b$y
bc <- cbind(lambda, lik)
sorted_bc <- bc[order(-lik),]
head(sorted_bc, n = 10)

##            lambda       lik
##  [1,]  0.06060606 -83600.29
##  [2,]  0.02020202 -83628.43
##  [3,]  0.10101010 -83675.75
##  [4,] -0.02020202 -83761.68
##  [5,]  0.14141414 -83853.26
##  [6,] -0.06060606 -84001.51
##  [7,]  0.18181818 -84131.28
##  [8,] -0.10101010 -84349.34
##  [9,]  0.22222222 -84508.22
## [10,] -0.14141414 -84806.57

Como vemos, los valores de $\lambda$ que maximizan esta función y que, por lo tanto, hacen que los residuales sean más simétricos son $\lambda=0.06$ y $\lambda=0.02$ . Para simplificar la exposición que sigue, supondremos que $\lambda=0$ .

Modelo transformado

Una vez que hemos identificado el valor de $\lambda$ , aplicamos la transformación que corresponda. En nuestro ejemplo, hemos obtenido que un modelo con $\lambda=0$ , el cual implica una transformación logarítmica es adecuado. Reestimamos el modelo una vez aplicada esta transformación.

mod.lrm_bc <- lm(log(exp_tot)~age+female, data=db, subset=(exp_tot>0))
smod.lrm_bc <- summary(mod.lrm_bc)

Observamos los residuales del modelo estimado en un histograma. Mucho más simétricos, ¿no es así?

hist(mod.lrm_bc$residuals)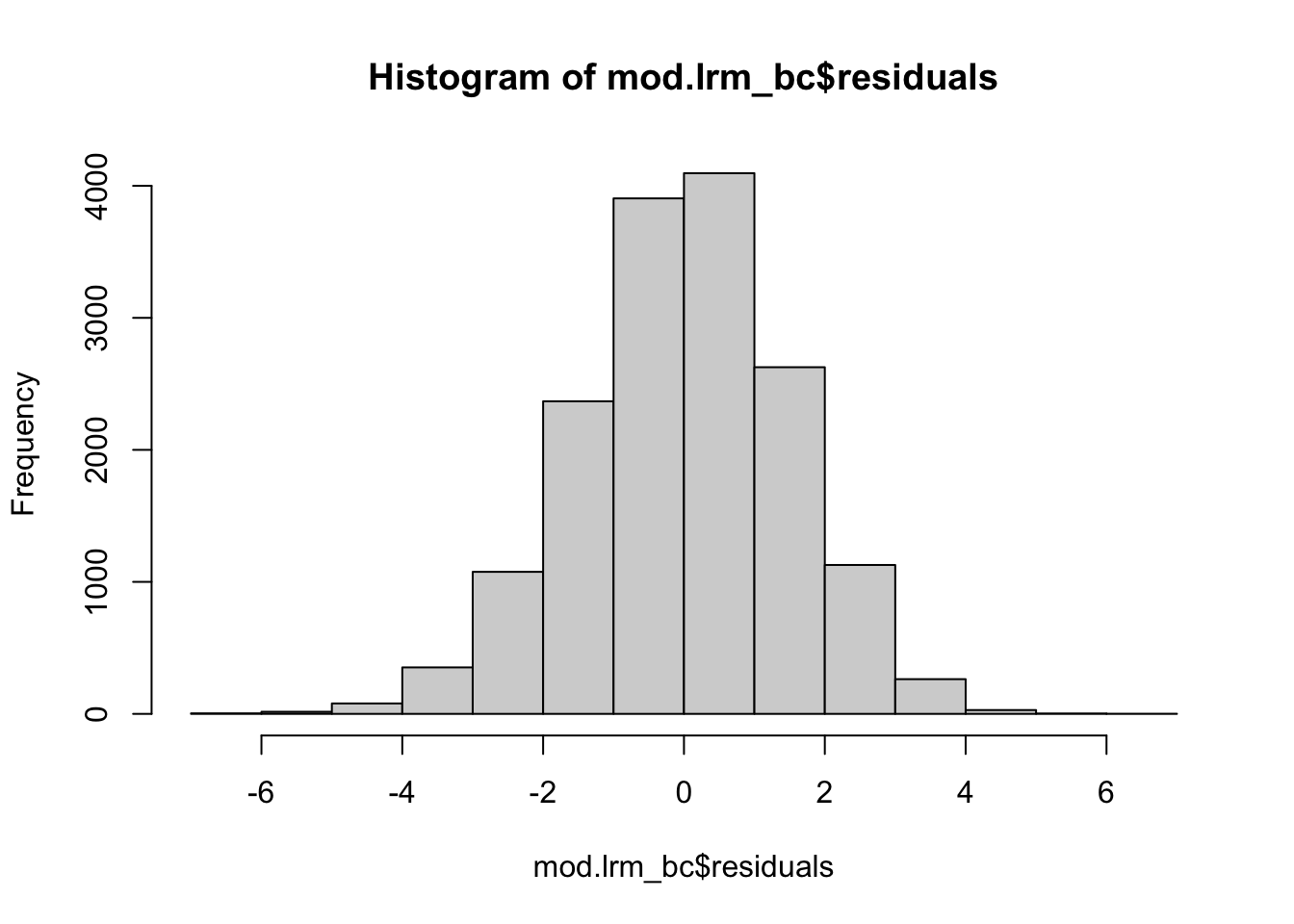

Comparamos los cuantiles de los residuales estandarizados contra los de una distribución normal. Como puedes ver, estos dos son mucho más cercanas unos de los otros.

qqPlot(rstandard(mod.lrm_bc))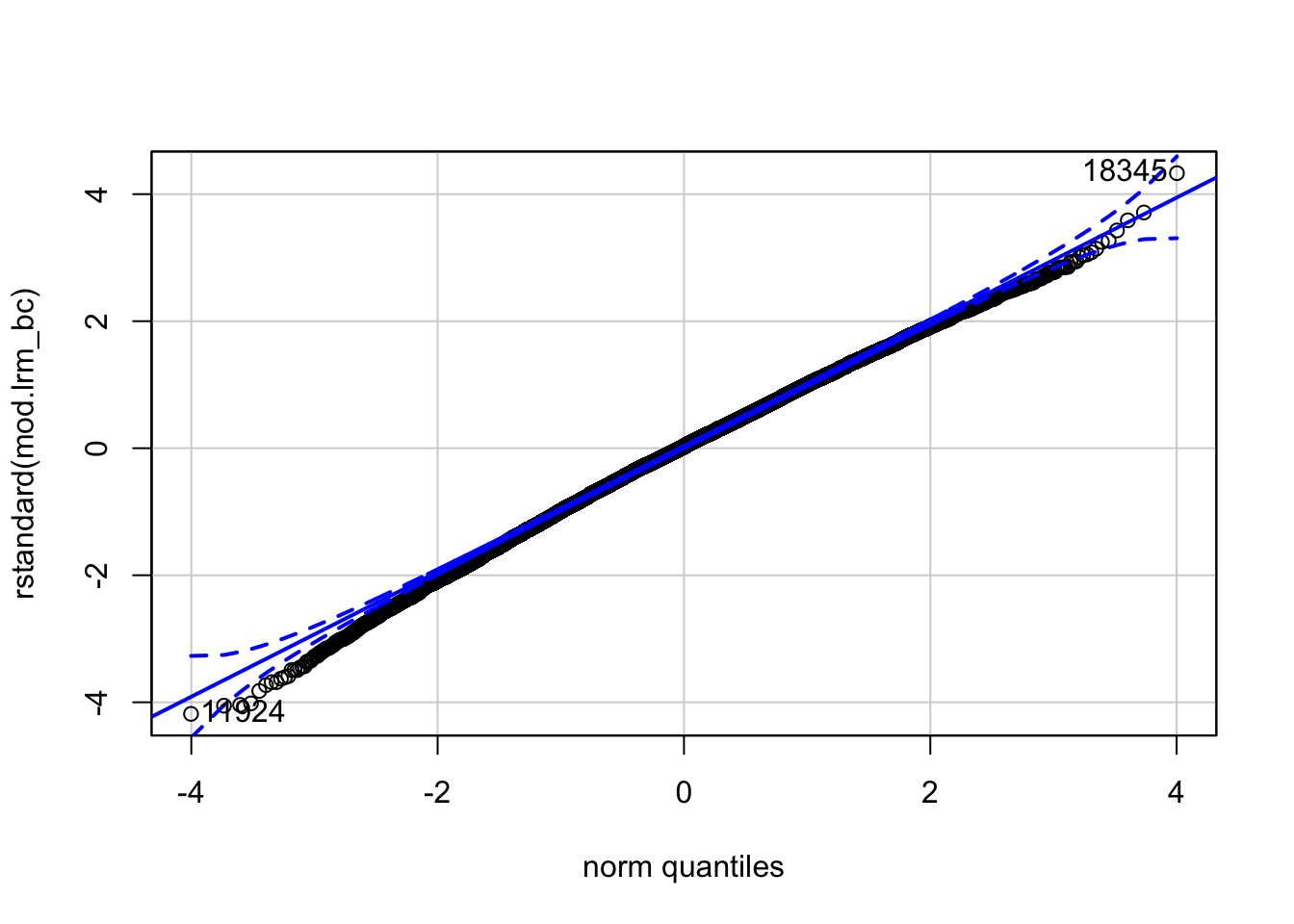

## 18345 11924 
## 15107  9896

Finalmente, calculamos los coeficientes de asimetría y curtósis de los residuales. Claramente, estos se acercan mucho más a los valores usuales para una distribición normal.

skewness(mod.lrm_bc$residuals)

## [1] -0.1786823

kurtosis(mod.lrm_bc$residuals)

## [1] 3.110932

Transformaciones Box-Cox y los modelos lineales generalizados

En el ejemplo anterior, vimos que una transformación logaritmica de la variable dependiente (es decir, la estimación de un modelo log-lin) hace que los residuales del modelo sean más simétricos y, en general, que estos estén más cerca de satisfacer los supuestos de Gauss-Markov. Pero, una vez estimado el modelo transformado, tendríamos que regresar el valor de $y$ a su escala original para su correcta interpretación. Para ser más concretos, el modelo que hemos considerado aquí es:

$\ln(y_i)=\boldsymbol{\beta} \mathbf{x_i} + \varepsilon_i,$ por lo que:

$\mathbb{E}\{\ln(y_i)|\mathbf{x_i}\} = \boldsymbol{\beta} \mathbf{x_i}$

Una vez estimado el modelo, nuestro objetivo es recuperar el valor de $\mathbb{E}(y_i|\mathbf{x_i})$ . ¿Cómo hacemos esto? La pregunta parece tener una respuesta trivial, pero nota que:

$\mathbb{E}(y_i|\mathbf{x_i}) \neq \exp\{ \boldsymbol{\beta} \mathbf{x_i}\}$ ¿Por qué? Simplemente porque el $\mathbb{E}(y_i|\mathbf{x_i})$ también depende de la exponencial del error. En particular, es fácil demostrar que:

$\mathbb{E}(y_i|\mathbf{x_i}) = \exp\{ \boldsymbol{\beta} \mathbf{x_i}\} \times \mathbb{E}(\exp\{\varepsilon_i \}| \mathbf{x_i})$ Es precisamente el término $\mathbb{E}(\exp\{\varepsilon_i \}| \mathbf{x_i})$ el que no nos deja recuperar el valor de $\mathbb{E}(y_i|\mathbf{x_i})$ luego de una estimación por mínimos cuadrados ordinarios (a pesar de que este puede ser tan pequeño que podemos ignorarlo). ¿Entonces?

Una opción es considerar un modelo lineal generalizado con una función de conexión logarítimica. A diferencia del modelo que aquí hemos visto, un modelo lineal generalizado nos permite encontrar un estimador de $\ln\{\mathbb{E}(y_i|\mathbf{x_i})\}$ . Entonces, en este caso tendríamos que:

$\mathbb{E}(y_i|\mathbf{x_i}) = \exp\{ \boldsymbol{\beta} \mathbf{x_i}\},$ que es justamente el valor que estamos buscando. En nuestro ejemplo tenemos:

mod.glm <- glm(exp_tot~age+female, family=gaussian(link="log"), data=db, subset =(exp_tot>0) )
smod.glm <- summary(mod.glm)
print(smod.glm)

## 
## Call:
## glm(formula = exp_tot ~ age + female, family = gaussian(link = "log"), 
##     data = db, subset = (exp_tot > 0))
## 
## Deviance Residuals: 
##    Min      1Q  Median      3Q     Max  
## -10986   -3357   -2093     -94  437920  
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 7.0414126  0.0678460 103.785   <2e-16 ***
## age         0.0257328  0.0009939  25.890   <2e-16 ***
## female1     0.0769795  0.0340328   2.262   0.0237 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for gaussian family taken to be 107480536)
## 
##     Null deviance: 1.7930e+12  on 15945  degrees of freedom
## Residual deviance: 1.7135e+12  on 15943  degrees of freedom
## AIC: 340144
## 
## Number of Fisher Scoring iterations: 8

La lectura de los coeficientes de este modelo y el de los coeficientes del modelo estimado por mínimos cuadrados ordinarios para el $\ln(y)$ es la misma.

Una ventaja adicional de los modelos lineales generalizados es que nos permiten tomar en cuenta la heteroscedasticidad en los residuales mediante una elección adecuada de la distribición de la varianza de los residuales. En el ejemplo anterior hemos seleccionado una distribición normal, pero otras distribuciones son posibles.

Última actualización: 26-08-2020.

Econometría & Co.