Modelos lineales generalizados

Tue, Aug 18, 2020 9-minute read

La familia lineal exponencial

Comenzamos definiendo al grupo de densidades pertencientes a la familia lineal exponencial. Sea $F_Y(y|\mu)$ una función de distribución con un único parámetro, $\mu$ . Se dice que esta pertenece a la familia exponencial si su función de densidad puede expresarse como:

$f_Y(y|\mu)=\exp\left\{a(\mu)+b(y)+c(\mu)y\right\},$ donde $\mu = \mathbb{E}(y)$ . Se puede mostrar que para esta parametrización:

$\begin{aligned} \mathbb{E}(y) &= -[c'(\mu)]^{-1}a'(\mu) \\ \mathbb{V}(y) &= [c'(\mu)]^{-1} \end{aligned}$

Dependiendo de las funciones $a(\cdot)$ y $c(\cdot)$ podemos encontrar diferentes funciones de densidad en esta familia. El término $b(y)$ es un elemento que asegura que la suma de probabilides sume 1. El término $\exp\left\{a(\mu)+c(\mu)y\right\}$ es una función exponencial que es lineal en $y$ . Algunos miembros importantes de esta familia son la distribución normal, la Bernoulli, la exponencial, la Poisson, entre otras.

Modelos lineales generalizados

Como sabemos, el procedimiento de mínimos cuadrados ordinarios resulta en estimadores que son insesgados, eficientes y consistentes, siempre y cuando se cumplan los supuestos del modelo de regresión lineal y, específicamente, los supuestos de Gauss Markov sobre el error. Sin embargo, en la práctica, es muy común que algunos de estos supuestos no se satisfagan. Por ejemplo, cuando la variable dependiente está sesgada o es binaria, un modelo de regresión lineal podría resultar en predicciones incoherentes, así como en residuales heteroscedásticos. Una solución a estos problemas consiste en considerar otra clase de modelos más generales que el modelo de regresión lineal. Estos son los modelos lineales generalizados (Nelder - Wedderburn, 1972), los cuales nos permiten ampliar la gama de distribuciones de la variable de respuesta (la variable dependiente) a todas aquellas que pertenezcan a la familia exponencial.

Los modelos lineales generalizados permiten que el valor esperado de la variable dependiente, $y$ , sea igual a una función de $\boldsymbol{\beta} \mathbf{x}$ , donde, como siempre, $\boldsymbol{\beta}$ es el vector de coeficientes a estimar y $\mathbf{x}$ es el vector de variables explicativas. Esta función se conoce como función de conexión. Naturalmente, si la función de conexión es la identidad, el modelo resultante es el de regresión lineal que conocemos.

Para ser más concretos, consideremos los supuestos que deben satisfacen los modelos lineales generalizados:

Existe una función índice, $\boldsymbol{\beta} \mathbf{x}$ , que permite identificar la relación entre un grupo de variables explicativas, $\mathbf{x}$ y una variable dependiente, $y$ . Esta función índice es lineal en sus parámetros, $\boldsymbol{\beta}$ , pero puede ser no lineal en sus variables (por ejemplo, en el caso de variables polinómicas y/o interactivas).
Existe una función de conexión, $g(\cdot)$ que indica el tipo de relación que existe entre la función índice y el valor esperado de la variable dependiente:

$\boldsymbol{\beta} \mathbf{x} = g\left\{\mathbb{E}(y_i | \mathbf{x}\right\}$ Nota que:

$\mu_i = \mathbb{E}(y_i | \mathbf{x}) = g^{-1}(\boldsymbol{\beta} \mathbf{x})$ Por ejemplo, si el valor esperado de $y$ es una función exponencial de $\boldsymbol{\beta} \mathbf{x}$ , entonces la función de conexión es el logaritmo natural.

La varianza de $y_i$ , $\nu_i = \mathbb{V}(y_i)$ , es una función de $\mu_i$ .
La variable dependiente, $y$ , proviene de alguna de las distribuciones de la familia exponencial.

Algunas combinaciones posibles para variables dependientes continuas son:

Conexión	Función de conexión $g(\cdot)$	Valor esperado
Identidad	$\boldsymbol{\beta} \mathbf{x} = \mu_i$	$\mu_i = \boldsymbol{\beta} \mathbf{x}$
Potencia	$\boldsymbol{\beta} \mathbf{x} = \mu_i^{1/\delta}$	$\mu_i = (\boldsymbol{\beta} \mathbf{x})^\delta$
Logaritmo	$\boldsymbol{\beta} \mathbf{x} = \ln( \mu_i)$	$\mu_i = \exp(\boldsymbol{\beta} \mathbf{x})$

Distribución	Varianza	Potencia
Gaussiana	$\nu_i \neq f(\mu)$	0
Poisson	$\nu_i \propto \mu$	1
Gamma	$\nu_i \propto \mu^2$	2
Gaussiana inversa	$\nu_i \propto \mu^3$	3

Los modelos lineales generalizados se estiman mediante el método de máxima verosimilitud.

Ejemplos de estimación con modelos lineales generalizados

Para los siguientes ejemplos, estaremos utilizando los siguientes paquetes de R:

# Instalar paquetes si es necesario
# install.packages("tidyverse")

# Leer paquetes
library(tidyverse)

## ── Attaching packages ──────────────── tidyverse 1.3.0 ──

## ✓ ggplot2 3.3.2     ✓ purrr   0.3.4
## ✓ tibble  3.0.1     ✓ dplyr   1.0.0
## ✓ tidyr   1.1.0     ✓ stringr 1.4.0
## ✓ readr   1.3.1     ✓ forcats 0.5.0

## ── Conflicts ─────────────────── tidyverse_conflicts() ──
## x dplyr::filter() masks stats::filter()
## x dplyr::lag()    masks stats::lag()

Consideremos una muestra del Medical Expenditure Panel Survey 2004 de los Estados Unidos. Tómate un tiempo para analizar la base de datos, así como para realizar un análisis de estadística descriptiva.

db <- read_csv("https://raw.githubusercontent.com/amosino/courses--econometria/master/econometria_salud/econometria_salud--datos/MEPSData.csv")

## Parsed with column specification:
## cols(
##   .default = col_double(),
##   famidyr = col_character(),
##   hieuidx = col_character(),
##   female = col_character(),
##   race_bl = col_character(),
##   race_oth = col_character(),
##   eth_hisp = col_character(),
##   ed_hs = col_character(),
##   ed_hsplus = col_character(),
##   ed_col = col_character(),
##   reg_midw = col_character(),
##   reg_south = col_character(),
##   reg_west = col_character(),
##   anylim = col_character(),
##   ins_mcare = col_character(),
##   ins_mcaid = col_character(),
##   ins_unins = col_character(),
##   ins_dent = col_character()
## )

## See spec(...) for full column specifications.

Deseamos modelar la dependencia que existe entre los gastos totales en salud (exp_tot), los cuales juegan el papel de la variable dependiente, en función de la edad de la persona (age) y de su género (female). Esta es una variable dummy que vale Female si la observación es una mujer y Malesi es hombre. Aunque R no tiene ningún problema manejando variables dummy cuyas características estén codificadas como texto, podemos recodificar, si así lo deseamos, la variable female, tal que esta valga 1 si la observación es una mujer y 0 si es hombre.

db$female <- as.factor(as.numeric(db$female=="Female"))

Un histograma de la variable dependiente revela que esta está muy sesgada hacia la izquierda, lo que indica que el método de los mínimos cuadrados ordinarios podría no ser el mejor método de estimación.

hist(db$exp_tot)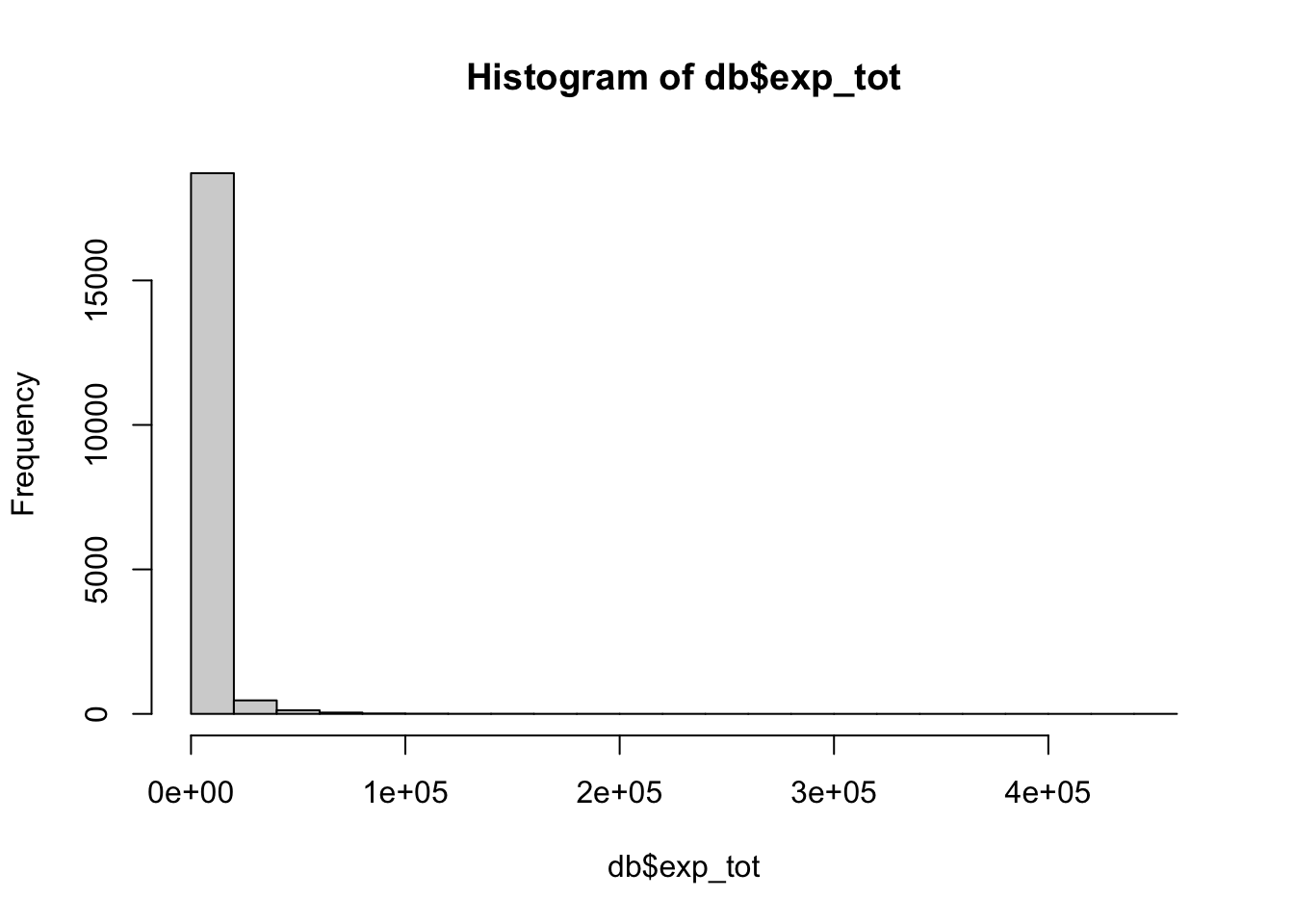

De hecho, podemos correr una regresión por el método de los MCO y recuperar sus residuales. ¿Te parece que estos cumplen con los supuestos de Gauss-Markov?

mod.lrm <- lm(exp_tot~age+female, data=db, subset=(exp_tot>0))
smod.lrm <- summary(mod.lrm)
print(smod.lrm)

## 
## Call:
## lm(formula = exp_tot ~ age + female, data = db, subset = (exp_tot > 
##     0))
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
##  -9422  -3676  -1968     62 438341 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -1819.043    256.984  -7.078 1.52e-12 ***
## age           125.064      4.669  26.787  < 2e-16 ***
## female1       624.556    167.018   3.739 0.000185 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 10370 on 15943 degrees of freedom
## Multiple R-squared:  0.04373,    Adjusted R-squared:  0.04361 
## F-statistic: 364.5 on 2 and 15943 DF,  p-value: < 2.2e-16

res2 <- residuals(mod.lrm)^2
hist(res2)

Ahora, consideremos la estimación de los coeficientes considerando alguna especificación entre los modelos lineales generalizados. Para comenzar utilicemos una función de conexión identidad con varianza gaussiana. Este, por definición, tendría que resultar en los mismos estimadores de MCO:

mod1.glm <- glm(exp_tot~age+female, data=db, subset =(exp_tot>0))
smod1.glm <- summary(mod1.glm)
print(smod1.glm)

## 
## Call:
## glm(formula = exp_tot ~ age + female, data = db, subset = (exp_tot > 
##     0))
## 
## Deviance Residuals: 
##    Min      1Q  Median      3Q     Max  
##  -9422   -3676   -1968      62  438341  
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -1819.043    256.984  -7.078 1.52e-12 ***
## age           125.064      4.669  26.787  < 2e-16 ***
## female1       624.556    167.018   3.739 0.000185 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for gaussian family taken to be 107543722)
## 
##     Null deviance: 1.7930e+12  on 15945  degrees of freedom
## Residual deviance: 1.7146e+12  on 15943  degrees of freedom
## AIC: 340154
## 
## Number of Fisher Scoring iterations: 2

Ahora, consideremos un modelo con una función de conexión logaritmica y una varianza con distribución gaussiana. Esta interpretación es la misma a la de un modelo de regresión no lineal con media exponencial, o bien a la de un modelo log-lin. De hecho, ¿cuál será la diferencia entre un modelo lineal generalizado con conexión logarítmica a un modelo log-lin?

mod2.glm <- glm(exp_tot~age+female, family=gaussian(link="log"), data=db, subset =(exp_tot>0) )
smod2.glm <- summary(mod2.glm)
print(smod2.glm)

## 
## Call:
## glm(formula = exp_tot ~ age + female, family = gaussian(link = "log"), 
##     data = db, subset = (exp_tot > 0))
## 
## Deviance Residuals: 
##    Min      1Q  Median      3Q     Max  
## -10986   -3357   -2093     -94  437920  
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 7.0414126  0.0678460 103.785   <2e-16 ***
## age         0.0257328  0.0009939  25.890   <2e-16 ***
## female1     0.0769795  0.0340328   2.262   0.0237 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for gaussian family taken to be 107480536)
## 
##     Null deviance: 1.7930e+12  on 15945  degrees of freedom
## Residual deviance: 1.7135e+12  on 15943  degrees of freedom
## AIC: 340144
## 
## Number of Fisher Scoring iterations: 8

Los resultados muestran que los gastos en salud se incrementan con la edad y son mayores para las mujeres. Dado que la media condicional tiene forma exponencial, los coeficientes pueden interpretarse directamente como cambios porcentuales. Entonces, los gastos en salud se incrementan en un 2.6% con cada año adicional de vida, controlando el resultado por el género. Los resultados de la estimación también muestran que las mujeres gastan 8% más que los hombres [0.08 = exp(0.077)-1], controlando el resultado por la edad.

Como tercer ejemplo, consideremos un modelo con una función de conexión logaritmica, pero una varianza con distribución gamma. Esto implica que la varianza de los gastos en salud es proporcional al cuadrado de su media.

mod3.glm <- glm(exp_tot~age+female, family=Gamma(link="log"), data=db, subset=(exp_tot>0))
smod3.glm <- summary(mod3.glm)
print(smod3.glm)

## 
## Call:
## glm(formula = exp_tot ~ age + female, family = Gamma(link = "log"), 
##     data = db, subset = (exp_tot > 0))
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -3.5466  -1.5229  -0.8463  -0.0129  19.3542  
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 6.835698   0.066017 103.544  < 2e-16 ***
## age         0.027951   0.001199  23.305  < 2e-16 ***
## female1     0.208600   0.042906   4.862 1.17e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for Gamma family taken to be 7.097201)
## 
##     Null deviance: 37405  on 15945  degrees of freedom
## Residual deviance: 33478  on 15943  degrees of freedom
## AIC: 292919
## 
## Number of Fisher Scoring iterations: 8

Nuevamente, los resultados muestran que los gastos en salud se incrementan con la edad y son mayores para las mujeres. A diferencia del ejemplo anterior, ambos coeficientes son significativos al 0.1%. Los gastos se incrementan en alrededor del 2.8% con cada año adicional de vida y las mujeres gastan alrededor de 23% más que los hombres. Nota la gran diferencia en el valor de este coeficiente.

Selección del modelo

Para seleccionar entre modelos, podemos utilizar los criterios de información de Akaike y Bayesiano. Esto se hace muy simplemente en R.

AIC.m1 <- AIC(mod1.glm, k=2)
BIC.m1 <- BIC(mod1.glm)
AIC.m2 <- AIC(mod2.glm, k=2)
BIC.m2 <- BIC(mod2.glm)
AIC.m3 <- AIC(mod3.glm, k=2)
BIC.m3 <- BIC(mod3.glm)
l.AIC <- c(AIC.m1, AIC.m2, AIC.m3)
l.BIC <- c(BIC.m1, BIC.m2, BIC.m3)
IC <- data.frame("AIC" = l.AIC, "BIC" = l.BIC)
print(IC)

##        AIC      BIC
## 1 340153.7 340184.4
## 2 340143.8 340174.5
## 3 292919.2 292949.9

Estos resultados implican que, claramente, el tercer modelo, al tener valores más pequeños tanto para el AIC como para el BIC, es el mejor.

Por último, diremos que no existe forma simple de elegir la distribución de la varianza en un modelo lineal generalizado. Sin embargo, sí existen formas que nos ayudan a elegir la función de conexión. Una de estas es la transformación de Box-Cox, cuyo análisis dejaremos para más adelante.

Última actualización: 20-08-2020.

Econometría & Co.

Modelos lineales generalizados

La familia lineal exponencial

Modelos lineales generalizados

Ejemplos de estimación con modelos lineales generalizados

Selección del modelo