Regresión de Poisson: teoría

Recuerda que, si una variable aleatoria $y_i$ sigue una distribución de Poisson con intensidad (o parámetro) $\mu$, su función de densidad es:

$\mathbb{P}(y_i) = \frac{e^{-\mu} \mu^{y_i}}{y_i!}, \ y=0,1,\dots$ Se puede demostrar que:

$\begin{aligned} \mathbb{E}(y_i) = \mu \\ \mathbb{V}(y_i) = \mu \end{aligned}$

Además, también puede demostrarse que, para una distribución de Poisson, el número de sucesos que ocurren en intervalos de tiempo disjuntos son variables aleatorias independientes.

Para derivar el modelo de regresión de Poisson, permitimos que el parámetro de intensidad varíe entre observaciones (por lo que tenemos $\mu_i$ en lugar de la constante $\mu$). Este se usa para parametrizar la relación entre la variable dependiente $y_i$ y el vector de regresores, $\mathbf{x}$. En particular, suponemos que:

$\mu_i=\exp\{\mathbf{x}\boldsymbol{\beta}\},$ donde $\boldsymbol{\beta}$ es, como siempre, un vector de coeficientes de dimensión $k\times 1$. Naturalmente, esta especificación implica que:

$\begin{aligned} \mathbb{E}(y_i|\mathbf{x}) = \mu_i = \exp\{\mathbf{x}\boldsymbol{\beta}\} \\ \mathbb{V}(y_i|\mathbf{x}) = \mu_i = \exp\{\mathbf{x}\boldsymbol{\beta}\}. \end{aligned}$

Estas relaciones implican:

1. Los coeficientes del modelo de regresión de Poisson pueden interpretarse como semielasticidaddes. Más precisamente:

$\frac{\partial \ln \mathbb{E}(y_i|\mathbf{x})}{\partial x_j}=\beta_j$ Entonces, un cambio de una unidad en la variable $x_j$ implica un cambio en $y_i$ de $\beta_j \%$.

2. El modelo de regresión de Poisson es intrínsecamente heteroscedástico.

Los coeficientes de un modelo de regresión de Poisson se estiman utilizando el procedimiento de máxima verosimilitud. Para construir la función de verosimilitud usamos las relaciones anteriores, el supuesto de independencia entre observaciones y el hecho que la distribución de Poisson pertenece a la familia exponencial. Tenemos entonces que:

$\mathcal{L}(\boldsymbol{\beta})=\sum_{i=1}^{n}\left\{y_i \mathbf{x}\boldsymbol{\beta}-\exp(\mathbf{x}\boldsymbol{\beta})-\ln(y_i!)\right\}$ Las condiciones de primer orden implican:

$\sum_{i=1}^{n}\left\{y_i-\exp(\mathbf{x}\boldsymbol{\beta})\right\}\mathbf{x}=0$

Estas serían las ecuaciones normales para el caso de una regresión de Poisson.

Regresión de Poisson: ejemplo

Para el siguiente ejemplo, estaremos utilizando los siguientes paquetes de R:

# Instalar paquetes si es necesario
# install.packages("tidyverse")
# install.packages("margins")
# install.packages("sandwich")
# install.packages("countreg", repos="http://R-Forge.R-project.org")
# install.packages("AER")

# Leer paquetes
library(tidyverse)

## Warning: package 'tidyverse' was built under R version 4.0.2

## ── Attaching packages ─────────────────────────── tidyverse 1.3.0 ──

## ✓ ggplot2 3.3.2     ✓ purrr   0.3.4
## ✓ tibble  3.0.1     ✓ dplyr   1.0.0
## ✓ tidyr   1.1.0     ✓ stringr 1.4.0
## ✓ readr   1.3.1     ✓ forcats 0.5.0

## ── Conflicts ────────────────────────────── tidyverse_conflicts() ──
## x dplyr::filter() masks stats::filter()
## x dplyr::lag()    masks stats::lag()

library(margins)

## Warning: package 'margins' was built under R version 4.0.2

library(sandwich)
library(countreg)

## Loading required package: MASS

## 
## Attaching package: 'MASS'

## The following object is masked from 'package:dplyr':
## 
##     select

library(AER)

## Warning: package 'AER' was built under R version 4.0.2

## Loading required package: car

## Loading required package: carData

## 
## Attaching package: 'car'

## The following object is masked from 'package:dplyr':
## 
##     recode

## The following object is masked from 'package:purrr':
## 
##     some

## Loading required package: lmtest

## Warning: package 'lmtest' was built under R version 4.0.2

## Loading required package: zoo

## 
## Attaching package: 'zoo'

## The following objects are masked from 'package:base':
## 
##     as.Date, as.Date.numeric

## Loading required package: survival

Consideremos una muestra del Medical Expenditure Panel Survey 2004 de los Estados Unidos. Tómate un tiempo para analizar la base de datos, así como para realizar un análisis de estadística descriptiva.

db <- read_csv("https://raw.githubusercontent.com/amosino/courses--econometria/master/econometria_salud/econometria_salud--datos/MEPSData.csv")

## Parsed with column specification:
## cols(
##   .default = col_double(),
##   famidyr = col_character(),
##   hieuidx = col_character(),
##   female = col_character(),
##   race_bl = col_character(),
##   race_oth = col_character(),
##   eth_hisp = col_character(),
##   ed_hs = col_character(),
##   ed_hsplus = col_character(),
##   ed_col = col_character(),
##   reg_midw = col_character(),
##   reg_south = col_character(),
##   reg_west = col_character(),
##   anylim = col_character(),
##   ins_mcare = col_character(),
##   ins_mcaid = col_character(),
##   ins_unins = col_character(),
##   ins_dent = col_character()
## )

## See spec(...) for full column specifications.

Deseamos modelar el número de visitas al consultorio médico (use_off), la cual juega el papel de la variable dependiente y es, claramente, una variable de conteo, en función de la edad de la persona (age) y de su género (female). Esta es una variable dummy que vale Female si la observación es una mujer y Malesi es hombre. Aunque R no tiene ningún problema manejando variables dummy cuyas características estén codificadas como texto, podemos recodificar, si así lo deseamos, la variable female, tal que esta valga 1 si la observación es una mujer y 0 si es hombre.

db$female <- as.factor(as.numeric(db$female=="Female"))

Un histograma de la variable dependiente revela que esta está muy sesgada hacia la izquierda. Esto, y el hecho de que la variable dependiente sea discreta, justifican la aplicación de un modelo de regresión de Poisson.

hist(db$use_off)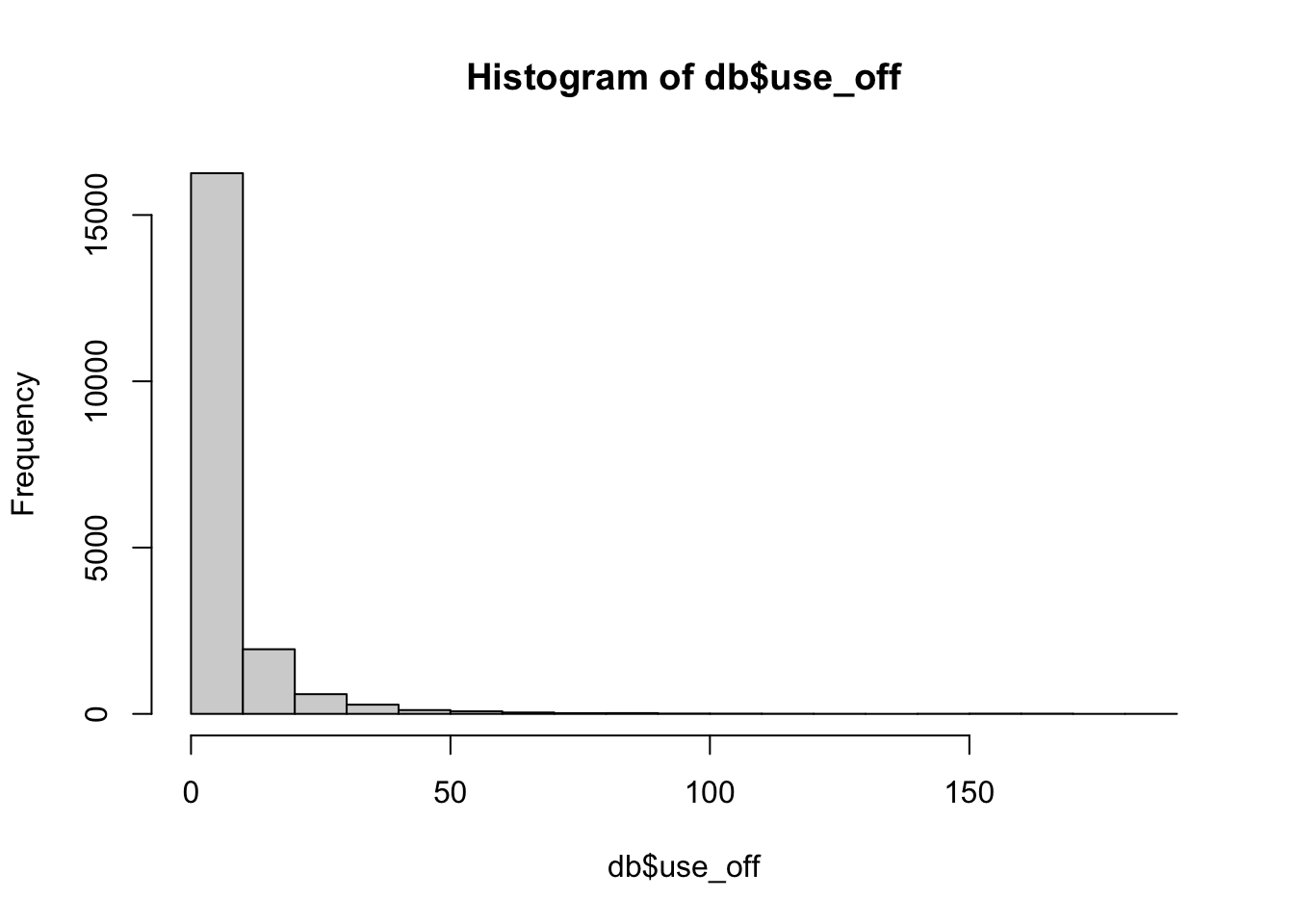

Dado que la distribución de Poisson pertenece a la familia de la exponencial, podemos estimar los coeficientes del modelo utilizando la función glm().

poisson.fit <- glm(use_off~ age + female, data=db, family = poisson)
summary(poisson.fit)

## 
## Call:
## glm(formula = use_off ~ age + female, family = poisson, data = db)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -5.6899  -2.5899  -1.5503   0.2515  29.3457  
## 
## Coefficients:
##              Estimate Std. Error z value Pr(>|z|)    
## (Intercept) 0.3201797  0.0099091   32.31   <2e-16 ***
## age         0.0242174  0.0001637  147.97   <2e-16 ***
## female1     0.4055818  0.0062865   64.52   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 216333  on 19385  degrees of freedom
## Residual deviance: 189439  on 19383  degrees of freedom
## AIC: 235916
## 
## Number of Fisher Scoring iterations: 6

Nota que el número de visitas al médico aumenta en un 2.5% con cada año adicional de vida [$100{\exp(0.0242)-1}$] y las mujeres visitan al médico 50% [$100{\exp(0.4055)-1}$] más que los hombres.

Aunque la interpretación de los coeficientes que acabamos de realizar es bastante intuitiva, en ocasiones resulta más interesante calcular los efectos marginales e incrementales con respecto a $y_i$ en lugar de los efectos marginales e incrementales con respecto a $\ln(y_i)$ (que es lo que acabamos de hacer). Los efectos marginales se calculan como:

$\frac{\partial \mathbb{E}(y_i|\mathbf{x})}{\partial x_j}=\beta_j \exp(\mathbb{x}\boldsymbol{\beta}),$ y los efectos incrementales:

$\Delta(y_i|\mathbf{x}, x_j)= \exp(\mathbb{x}\boldsymbol{\beta}|x_j=1)-\exp(\mathbb{x}\boldsymbol{\beta}|x_j=0)$

Como podemos ver, ambos cálculos dependen del valor que tomen las variables explicativas del modelo. Los valores de las variables en $\mathbb{x}$ pueden elegirse en función de la pregunta específica que deseamos responder. La opción más simple consiste en calcular el efecto marginal promedio y el efecto incremental promedio. En estas, se calculan los efectos marginales (o incrementales) para todos los individuos en la población y luego se calculan los promedios. En R podemos utilizar la función margins() del paquete del mismo nombre para hacer los cálculos de forma automática.

summary(margins(poisson.fit))

##   factor    AME     SE        z      p  lower  upper
##      age 0.1405 0.0010 135.3803 0.0000 0.1385 0.1426
##  female1 2.2673 0.0341  66.5309 0.0000 2.2005 2.3341

Así pues, el efecto marginal promedio para la variable age es 0.14. Es decir, en promedio, cada año adicional de vida implica visitar al médico 0.14 veces más. El efecto incremental de la variable female es 2.26. Esto quiere decir que las mujeres, en promedio, visitan al médico 2.26 veces más que los hombres.

Otra opción es evaluar los efectos marginales e incrementales en los valores promedio de las variables. Para esto, basta con agregar el argumento at a la función margins(). El siguiente bloque de código calcula el efecto marginal evaluando en la edad promedio y fijando el valor de la variable dummy en 1.

summary(margins(poisson.fit, at=list(age=mean(db$age)), variables="female"))

##   factor     age    AME     SE       z      p  lower  upper
##  female1 45.3609 2.0666 0.0313 65.9890 0.0000 2.0052 2.1280

Entonces, las mujeres de 45.36 años visitan al médico 2.066 veces en promedio.

Errores estándar robustos

Uno de los problemas a los que podríamos enfrentarnos al estimar un modelo de regresión de Poisson es que tanto la media como la varianza de $y_i$ son iguales a $\mu$. Sin embargo, no es poco frecuente de que los datos presenten sobre dispersión, es decir, que la varianza sea superior a la media. Esto conduce a errores estándar subestimados y, como consecuencia, valores t sobre estimados. En R, podemos realizar un test formal de sobre dispersión si utilizamos la función dispersiontest() del paquete AER. En esta, la hipótesis nula es la de equi dispersión. La hipótesis alternativa es que existe ya sea sobre dispersión o sub dispersión. Para revisar si existe sobre dispersión simplemente tecleamos:

dispersiontest(poisson.fit)

## 
##  Overdispersion test
## 
## data:  poisson.fit
## z = 16.757, p-value < 2.2e-16
## alternative hypothesis: true dispersion is greater than 1
## sample estimates:
## dispersion 
##   18.62108

Dado que el valor p de la prueba es inferior a $\alpha=1$, rechazamos la hipótesis nula en favor de la alternativa. Es decir, en nuestro modelo tenemos un problema de sobre dispersión.

Para enfrentar este problema, podemos calcular errores estándar robustos. Para esto, podemos utilizar la función vcovHC() que pertenece al paquete sandwich. El siguiente bloque de código hace los cálculos.

cov.m1 <- vcovHC(poisson.fit, type="HC0")
std.err <- sqrt(diag(cov.m1))
r.est <- cbind(Estimate= coef(poisson.fit), "Robust SE" = std.err,
               "Pr(>|z|)" = 2 * pnorm(abs(coef(poisson.fit)/std.err), lower.tail=FALSE),
               LL = coef(poisson.fit) - 1.96 * std.err,
               UL = coef(poisson.fit) + 1.96 * std.err)
r.est

##               Estimate   Robust SE     Pr(>|z|)         LL         UL
## (Intercept) 0.32017973 0.038473351 8.640591e-17 0.24477197 0.39558750
## age         0.02421735 0.000621169 0.000000e+00 0.02299986 0.02543484
## female1     0.40558180 0.028079739 2.737731e-47 0.35054551 0.46061809

Nota que el objeto r.est tiene como único objetivo guardar y presentar el pantalla los resultados. En estos se presentan los estimadores originales justo con sus errores estándar robustos, el estadístico p de la prueba de significancia individual y los intervalos de confianza al 95% para los coeficientes estimados.

Recuerda que la estimación con errores estándar robustos no resuelven el problema de la sobre dispersión, pero sí hacen que las pruebas de significancia sean confiables.

Grado de ajuste

Finalmente, es importante destacar que, aun cuando los parámetros estimados mediante un modelo de regresión de Poisson son consistentes, las estimaciones de los efectos marginales e incrementales y las probabilidades podrían ser inconsistentes. Para analizar el grado de ajuste de un modelo de regresión de Poisson podemos trazar un rootograma. Este representa la raiz cuadrada tanto de las frecuencias pronosticadas por el modelo como de las frecuencias empíricas (observadas) Las primeras se representan por puntos conectados por segmentos de línea y las segundas como un gráfico de barras.

Existen varias versiones de un rootograma tiene varias versiones. En su versión colgante, la barra cuelga de los puntos. Si la barra no llega al eje de las abscisas tenemos que la predicción de la frecuencia es superior a la frecuencia empírica. Por el contrario, si la barra corta el eje de las abscisas, el modelo predice una frecuencia inferior a la empírica. Naturalmente, el ajuste es mejor en tanto las barras justo toquen el eje de las abscisas.

En R podemos utilizar la función rootogram() que pertenece al paquete countreg. El uso de esta función es muy simple como se muestra a continuación.

rootogram(poisson.fit)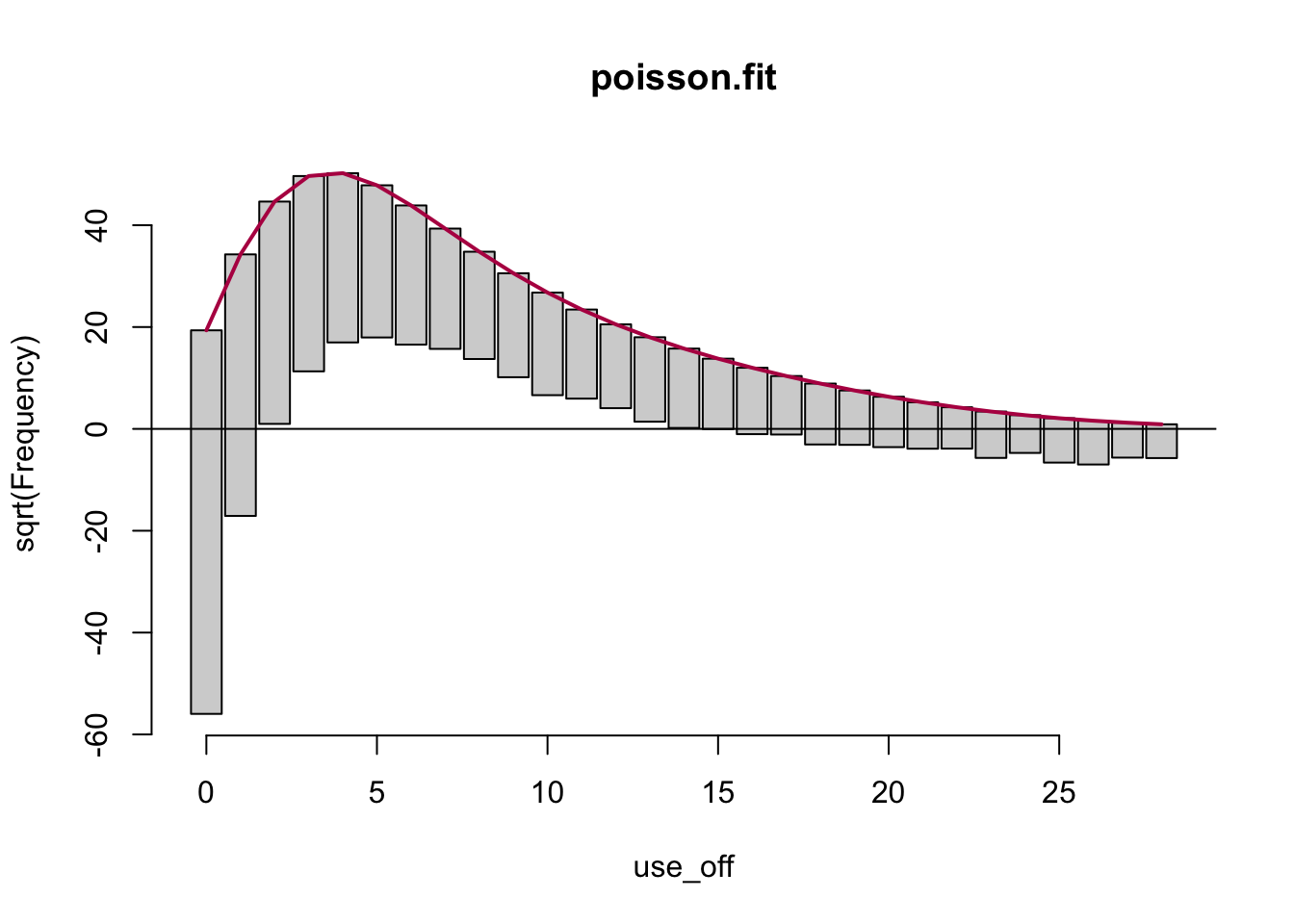

Como vemos, algunas de las frecuencias son subestimadas por el modelo, especialmente las que corresponden al evento 0 y 1 (visitas al médico). En cambio, los eventos en el centro de la distribución están sobre estimados.

Última actualización: 07-10-2020.