Cuantiles poblacionales

Consideremos una variable aleatoria, $y$, con función de distribución acumulada $F_y$. El $\tau$-ésimo cuantil poblacional de $y$, es el valor $y_\tau$ tal que:

$\tau = \mathbb{P}(y\leq y_\tau) = F_y(y_\tau)$ Por ejemplo, si $y_{0.75}=3$, entonces la probabilidad de que $y\leq 3=0.75$. De aquí obtenemos que:

$y_\tau = F_y^{-1}(\tau)$ Los cuantiles poblacionales más calculados en la práctica son: 1) la mediana, $\tau=0.5$, 2) el cuantil $\tau=0.75$ y 3) el cuantil $\tau=0.25$. Para la función de distribución normal estándar tenemos que $y_{0.5}=0$, $y_{0.95}=1.645$ y $y_{0.975}=1.960$.

En una regresión cuantílica, deseamos estimar el $\tau$-ésimo cuantil de $y$ como una función lineal de un vector de variables explicativas. Esto es: $Q_\tau(y|\mathbf{x})=\mathbf{x}\boldsymbol{\beta} = F_{y|\mathbf{x}}^{-1}(\tau)$. Para ver cómo se obtiene esta, consideremos un modelo lineal con heteroscedasticidad multiplicativa:

$\begin{aligned} y&=\mathbf{x}\boldsymbol{\beta} + u \\ u&=\mathbf{x}\boldsymbol{\alpha} \times \varepsilon \\ \varepsilon &\sim iid(0,\sigma^2) \end{aligned}$

Aquí, suponemos que $\mathbf{x}\boldsymbol{\alpha}>0$. Entonces, el $\tau$-ésimo cuantil poblacional de $y$ condicional a $\mathbf{x}$ es una función $y_\tau(\mathbf{x}, \boldsymbol{\beta},\boldsymbol{\alpha})$ tal que:

$\begin{aligned} \tau &= \mathbb{P}[y\leq y_\tau(\mathbf{x}, \boldsymbol{\beta},\boldsymbol{\alpha})] \\ &= \mathbb{P}[u \leq y_\tau(\mathbf{x}, \boldsymbol{\beta},\boldsymbol{\alpha})-\mathbf{x}\boldsymbol{\beta} ] \\ &= \mathbb{P}[\varepsilon \leq [y_\tau(\mathbf{x}, \boldsymbol{\beta},\boldsymbol{\alpha})-\mathbf{x}\boldsymbol{\beta}] /\mathbf{x}\boldsymbol{\alpha}] \\ &= F_\varepsilon\left([y_\tau(\mathbf{x}, \boldsymbol{\beta},\boldsymbol{\alpha})-\mathbf{x}\boldsymbol{\beta}] /\mathbf{x}\boldsymbol{\alpha}\right) \end{aligned}$

En esta ecuación hemos utilizado el hecho que: $u=y-\mathbf{x}\boldsymbol{\beta}$, $\varepsilon = u/\mathbf{x}\boldsymbol{\alpha}$ y $F_\varepsilon$ es la función de densidad acumulada de $\varepsilon$. De aquí obtenemos que $y_\tau(\mathbf{x}, \boldsymbol{\beta},\boldsymbol{\alpha})-\mathbf{x}\boldsymbol{\beta}] /\mathbf{x}\boldsymbol{\alpha} = F_\varepsilon^{-1}(\tau)$ tal que:

$\begin{aligned} y_\tau(\mathbf{x}, \boldsymbol{\beta},\boldsymbol{\alpha}) &= \mathbf{x}\boldsymbol{\beta} + \mathbf{x}\boldsymbol{\alpha} \times F_\varepsilon^{-1}(\tau) \\ &= \mathbf{x}(\boldsymbol{\beta} + \boldsymbol{\alpha}\times F_\varepsilon^{-1}(\tau) ) \end{aligned}$

Entonces, para el modelo lineal con hetersocedasticidad multiplicativa de la forma $u=\mathbf{x}\boldsymbol{\alpha} \times \varepsilon$, los cuantiles condicionales son lineales en $\mathbf{x}$. En el caso especial de homoscedasticidad, $\mathbf{x}\boldsymbol{\alpha}$ es igual a una constante y todos los cuantiles condicionales tienen la misma pendiente, pero diferente intercepto.

Cuantiles muestrales

Para calcular los cuantiles muestrales de una variable aleatoria $y$ tenemos dos opciones. La primera, la más común, consiste en ordenar los datos de menor a mayor. En este caso, el $q$-ésimo cuantil muestral, $\widehat{y}_\tau$, sería el $Nq$-ésimo valor más pequeño, donde $N$ es el tamaño de la muestra y $Nq$ se redondea al valor entero más cercano. Por ejemplo, si $N=97$, el cuantil $\tau=0.25$ sería la observación en la posición 25, ya que $97 \times 0.25=24.25$. La segunda opción es la de Koenker y Bassett (1978). Ellos mostraron que $\widehat{y}_\tau$ también puede encontrarse minimizando la siguiente expresión con respecto a $\beta$:

$\sum_{i:y_i\geq\beta}^N \tau |y_i - \beta | + \sum_{i:y_i < \beta}^N (1-\tau)|y_i - \beta|$ Esta segunda versión del cálculo de los cuantiles muestrales no es tan obvia. Sin embargo, es precisamente esta la que extender para el caso de una regresión lineal. En particular, los coeficientes estimados de una regresión para el $\tau$-ésimo cuantil, $\widehat{\boldsymbol{\beta}}_\tau$, es aquel que minimiza:

$Q_N(\boldsymbol{\beta_\tau}) = \sum_{i:y_i\geq \mathbf{x}\boldsymbol{\beta}}^N \tau |y_i - \mathbf{x}\boldsymbol{\beta}_\tau | + \sum_{i:y_i < \mathbf{x}\boldsymbol{\beta}}^N (1-\tau)|y_i - \mathbf{x}\boldsymbol{\beta}_\tau|$ En esta ecuación, hemos utilizado $\boldsymbol{\beta}_\tau$ en lugar de $\boldsymbol{\beta}$ para dejar en claro que los valores estimados de $\boldsymbol{\beta}$ dependen de la elección del cuantil $\tau$. Un caso especial es cuando fijamos $\tau=0.5$, en cuyo caso tenemos la conocida regresión en la mediana o estimación de mínimas desviaciones absolutas. Esta es muy popular debido principalmente a que es más robusta con respecto a los valores atípicos (outliers) que una regresión por mínimos cuadrados ordinarios, la cual puede interpretarse como una regresión en la media. (Recuerda, media y mediana no son lo mismo.) Esto es porque la regresión cuantílica “penaliza” los errores de forma lineal, mientras que la regresión MCO, al elevar los errores al cuadrado, lo que hace es darle mayor importancia precisamente a dichos valores, “penalizándolos” de forma cuadrática.

Ejemplo

Para el siguiente ejemplo, estaremos utilizando los siguientes paquetes de R:

# Instalar paquetes si es necesario
# install.packages("tidyverse")

# Leer paquetes
library(tidyverse)
library(quantreg)

Utilizaremos una regresión cuantílica para analizar el salario (Salary) de los jugadores de la MLB (liga de Beisbol en Estados Unidos) en diferentes cuentiles. Supondremos que este es una función de sus estadísticas, tales como: número de veces al bate (AtBat), número total de hits (Hits), el número de home-runs (HmRun), el número de base por bolas (Walks), número de años en la la liga (Years) y el número de put_outs (PutOuts).

db <- read_csv("https://raw.githubusercontent.com/amosino/courses--econometria/master/econometria_salud/econometria_salud--datos/BaseballData.csv")

Primero, observemos la distribución del salario (en logaritmos):

hist(log(db$Salary), prob=TRUE)
lines(density(log(db$Salary)))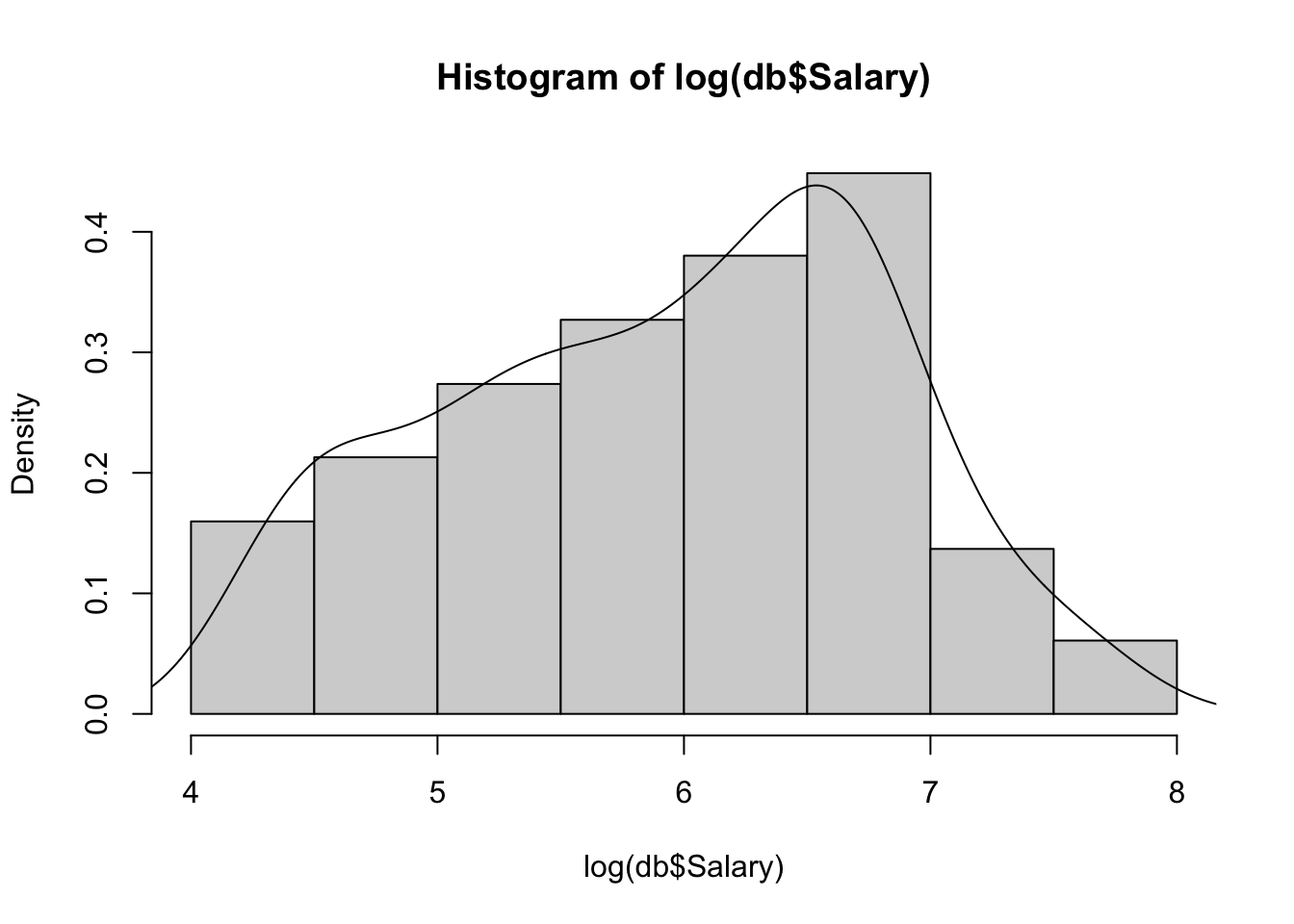

La gráfica que acabamos de obtener nos deja en claro que el comportamiento de los salarios podría ser diferente en cada uno de los cuantiles. Los cuantiles más utilizados pueden obtenerse mediante la función summary():

summary(log(db$Salary))

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   4.212   5.247   6.052   5.927   6.620   7.808

Entonces, el cuantil $\tau=0.25$, está determinado por el número 5.247. Esto implica que el primer 25% de los datos se encuentran debajo de este valor. La mediana ($\tau=0.5$), es el número que divide el conjunto de datos en dos partes: 50% de los datos se encuentran por debajo de 6.052 y el restante 50% se encuentran por encima.

Antes de modelar los determinantes del (log) del salario en cada uno de estos cuantiles, estimamos primero los coeficientes del modeloutilizando el método de los mínimos cuadrados ordinarios:

model.ols <- lm(log(Salary)~AtBat+Hits+HmRun+Walks+Years+PutOuts, data=db)
summary(model.ols)

## 
## Call:
## lm(formula = log(Salary) ~ AtBat + Hits + HmRun + Walks + Years + 
##     PutOuts, data = db)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -2.23228 -0.45066  0.05001  0.38638  3.12048 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  4.3694992  0.1334110  32.752  < 2e-16 ***
## AtBat       -0.0025781  0.0010372  -2.486  0.01357 *  
## Hits         0.0136637  0.0032213   4.242  3.1e-05 ***
## HmRun        0.0051472  0.0054003   0.953  0.34142    
## Walks        0.0071448  0.0023422   3.050  0.00253 ** 
## Years        0.0932264  0.0082137  11.350  < 2e-16 ***
## PutOuts      0.0003089  0.0001466   2.107  0.03605 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.6238 on 256 degrees of freedom
## Multiple R-squared:  0.5191, Adjusted R-squared:  0.5078 
## F-statistic: 46.06 on 6 and 256 DF,  p-value: < 2.2e-16

Los resultados nos indican, por ejemplo, que un hit adicional incrementa el salario promedio en 1.3% y cada año adicional del experiencia lo hace en 9.3%. En los datos se muestra que el número de home-runs parece no tener efecto en el salario promedio.

Ahora hagamos los cálculos en diferentes cuantiles. PAra esto utilizamos la función rq() del paquete quantreg. Por ejemplo, para el cuantil $\tau=0.25$. Nota que la sintaxis de la función rq() es muy parecida a la de lm(), excepto que en la primera es necesario especificar el argumento tau. También, nota que en la función summary() hemos especificado que los errores estándar de la regresión serán calculados utilizando el método bootstrap.

model.qr1 <- rq(log(Salary)~AtBat+Hits+HmRun+Walks+Years+PutOuts, data=db, tau=0.25)
summary(model.qr1, se = "boot")

## 
## Call: rq(formula = log(Salary) ~ AtBat + Hits + HmRun + Walks + Years + 
##     PutOuts, tau = 0.25, data = db)
## 
## tau: [1] 0.25
## 
## Coefficients:
##             Value    Std. Error t value  Pr(>|t|)
## (Intercept)  3.71999  0.11194   33.23073  0.00000
## AtBat       -0.00257  0.00118   -2.16761  0.03111
## Hits         0.01576  0.00393    4.01022  0.00008
## HmRun        0.00022  0.00593    0.03699  0.97052
## Walks        0.00902  0.00294    3.07433  0.00234
## Years        0.10389  0.00921   11.27772  0.00000
## PutOuts     -0.00015  0.00026   -0.58492  0.55911

Como podemos verun hit adicional incrementa el salario del cuantil 0.25 en 1.5% y cada año adicional del experiencia lo hace en 10.3%. Este efecto parece ser mayor que en el caso del salario promedio. En el cuantil 0.25 el número de home-runs tampoco parece tener efecto en el salario.

Una de las ventajas de la función qr() es que nos permite introducir más de un valor de $\tau$ como argumento. Por ejemplo, estimamos los coeficientes para los cuantiles $\tau=0.5$ y $\tau=0.75$:

model.qr2 <- rq(log(Salary)~AtBat+Hits+HmRun+Walks+Years+PutOuts, data=db, tau=c(0.5, 0.75))
summary(model.qr2, se = "boot")

## 
## Call: rq(formula = log(Salary) ~ AtBat + Hits + HmRun + Walks + Years + 
##     PutOuts, tau = c(0.5, 0.75), data = db)
## 
## tau: [1] 0.5
## 
## Coefficients:
##             Value    Std. Error t value  Pr(>|t|)
## (Intercept)  4.07795  0.27921   14.60555  0.00000
## AtBat       -0.00254  0.00143   -1.77961  0.07633
## Hits         0.01503  0.00420    3.57935  0.00041
## HmRun        0.00244  0.00926    0.26388  0.79208
## Walks        0.00777  0.00358    2.16777  0.03110
## Years        0.10538  0.01618    6.51276  0.00000
## PutOuts      0.00046  0.00026    1.76505  0.07875
## 
## Call: rq(formula = log(Salary) ~ AtBat + Hits + HmRun + Walks + Years + 
##     PutOuts, tau = c(0.5, 0.75), data = db)
## 
## tau: [1] 0.75
## 
## Coefficients:
##             Value    Std. Error t value  Pr(>|t|)
## (Intercept)  4.66319  0.15651   29.79537  0.00000
## AtBat       -0.00174  0.00135   -1.28165  0.20112
## Hits         0.01106  0.00402    2.75036  0.00638
## HmRun        0.01687  0.00599    2.81673  0.00523
## Walks        0.00616  0.00251    2.45259  0.01485
## Years        0.08664  0.01363    6.35838  0.00000
## PutOuts      0.00040  0.00020    2.01580  0.04487

Un resultado interesante es que el número de home-runs no es estadísticamente significativo para los cuantiles 0.25 y 0.5, pero sí lo es para el cuantil 0.75. En este punto, cada home-run adicional incrementa el salario en 1.6%. Entonces, los home-runs parecen tener importancia solo para los jugadores con salarios más altos.

Naturalmente, observar las tablas para todos los cuantiles de una distribución parece ser demasiado tedioso. Imagína, por ejemplo, que deseas analizar el efecto de las variables explicativas para los cuantiles 0.1, 0.2, …, 0.9. En este caso, las gráficas podrían ser más informativas que las tablas. Para esto, combinamos la función plot() con la función summary():

model.rq3<-rq(log(Salary)~AtBat+Hits+HmRun+Walks+Years+PutOuts, data=db, tau=seq(0.1, 0.9, by=0.1))
plot(summary(model.rq3))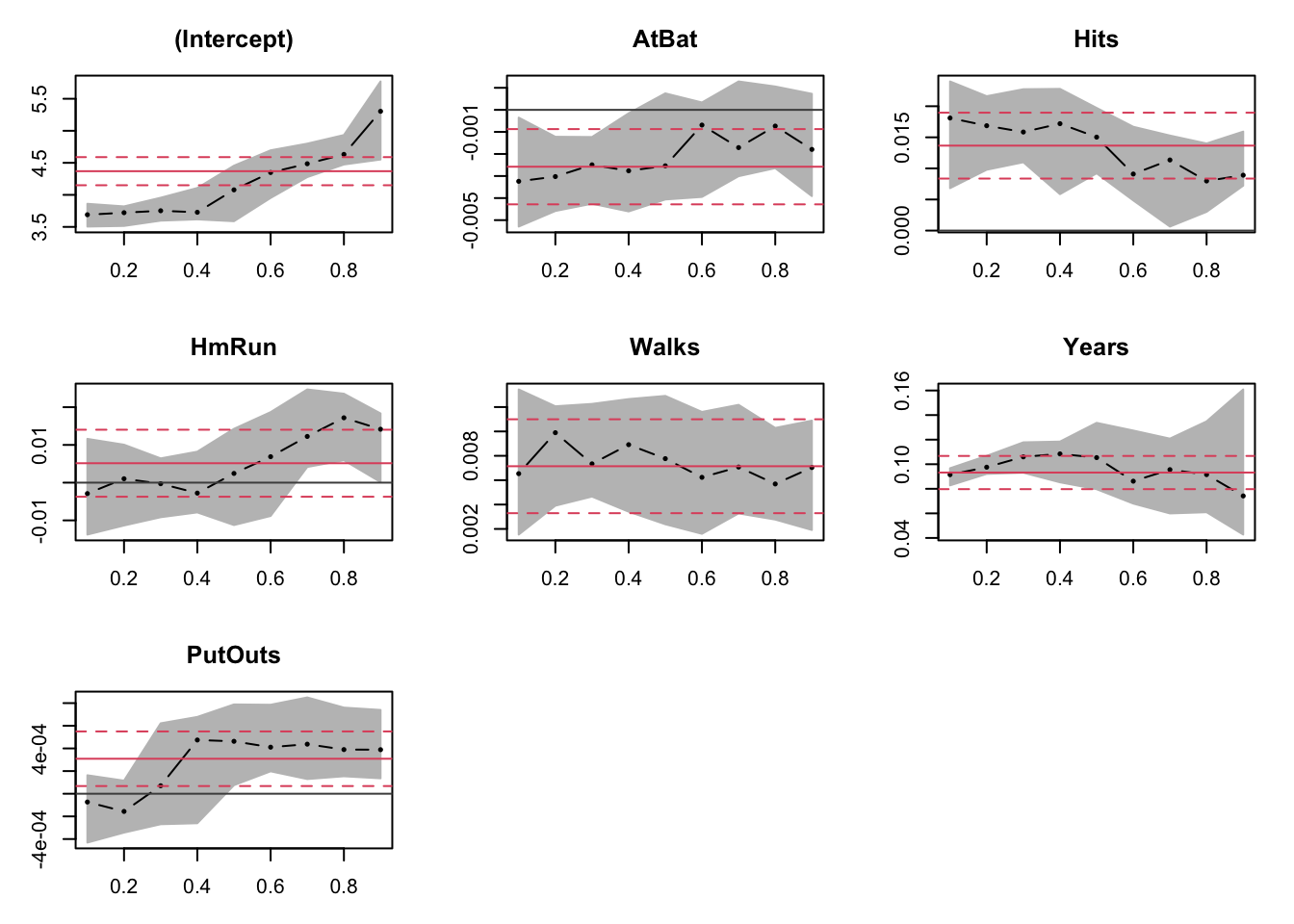

En cada una de las gráficas resultantes vemos varios elementos interesantes. La línea roja horizontal representa la estimación por MCO, y las líneas rojas punteadas son sus intervalos de confianza. Los puntos negros (conectados por pequeñas líneas) son las estimaciones mediante la regresión cuantílica y el área sombreada delimita sus intervalos de confianza. Comparando estos, podemos saber: 1) si existen diferencias estadísticas entre los coeficientes de la regresión cuantílica y los coeficientes de MCO. Si los intervalos de confianza de la regresión cuantílica caen dentro de los intervalos de confianza de MCO, entonces no hay razones para pensar que existen diferencias estadísticas suficientes que justifiquen la estimación por cuantiles. Esto parece ser el caso para nuestros datos. Algunas excepciones podrían ser el efecto de los home-runs para los cuantiles más altos y el número de put-outs para los cuantiles más bajos.