El modelo Tobit

Wed, Sep 2, 2020 8-minute read

En Estadística, la censura es el fenómeno que ocurre cuando el valor de una observación sólo se conoce parcialmente. Por ejemplo, podemos incluir personas de todos los niveles socioeconómicos en un estudio, pero, por razones de confidencialidad, aquellas con muy altos ingresos se reportan (codifican) todas como personas con ingresos superiores a, por ejemplo, $100,000 mensuales. La censura también puede ocurrir cuando hay observaciones fuera del rango de cierto instrumento de medida. Por ejemplo, si se utiliza un termómetro con un valor máximo de 100 grados para medir la temperatura en un experimento, para todas las observaciones que igualen o superen esos 100 grados sólo se sabe que se superó el umbral máximo de temperatura, pero no se sabe en qué medida.

En general, para un estudio econométrico tenemos datos censurados cuando tenemos información perdida para la variable dependiente, pero no para los regresores. Este fenómeno no debe confundirse con el de truncamiento. Con censura, se sabe que las observaciones censuradas superan cierto umbral (o están en cierto intervalo) y esa información parcial puede usarse a la hora de modelar estadísticamente el fenómeno. Con el truncamiento, las observaciones se descartan enteramente.

En esta entrada estudiaremos el modelo Tobit (James Tobin, 1958). Este está diseñado para estimar los coeficientes en un modelo con datos censurados. El modelo supone que existe una variable latente (no observable), y∗y^*. Esta depende linealmente de un vector de variables x\mathbf{x} y de un término de error, uiu_i:

y∗=xβ+uui∼N(0,σ2)\begin{aligned} y^*&=\mathbf{x}\boldsymbol{\beta}+\mathbf{u}\\ u_i &\sim \mathcal{N}(0,\sigma^2) \\ \end{aligned}

La variable observada, yy, es tal que:

y={y∗ si y∗>0− si y∗≤0y=\begin{cases} y^* & \ \text{si} \ y^*>0 \\ - & \ \text{si} \ y^*\leq 0\\ \end{cases} donde −- significa que esa observación particular se ha perdido (o ha sido recodificada). En la mayor parte de las aplicaciones suele fijarse y=0y=0.

Datos censurados: estimación por MCO

En lo que resta de esta entrada, estaremos utilizando los siguientes paquetes de R:

# Instalar paquetes si es necesario
# install.packages("ggplot2")
# install.packages("dplyr")
# install.packages("VGAM")

# Leer paquetes
library(ggplot2)
library(dplyr)
## 
## Attaching package: 'dplyr'
## The following objects are masked from 'package:stats':
## 
##     filter, lag
## The following objects are masked from 'package:base':
## 
##     intersect, setdiff, setequal, union
library(VGAM)
## Warning: package 'VGAM' was built under R version 4.0.2
## Loading required package: stats4
## Loading required package: splines

Para ver cuáles son las consecuencias de estimar un modelo con datos censurados utilizando el método de los mínimos cuadrados ordinarios, consideremos el siguiente experimento.

Sea el modelo verdadero:

yi∗=−40+1.2xi+ui,y^*_i = -40+1.2 x_i + u_i, donde la variable xix_i toma valores enteros entre 11 y 60 y uiu_i es una variable aleatoria normal con media 00 y varianza 100100. Una realización de valores para uiu_i y yi∗y_i^* puede calcularse como:

#Generación de datos
set.seed(123)
x<- seq(11,60,1)
u<-rnorm(length(x), 0,10)
y<- -40 + 1.2*x + u
db <- data.frame(x,y)

En este caso, la estimación del modelo por MCO se vería como:

#Visualización de datos
ggplot(data = db, aes(x = x, y = y)) +
geom_point(size = 2) +
geom_smooth(method = "lm", se = FALSE) +
theme_bw() +
labs(title = "Regresión OLS con los datos no censurados")
## `geom_smooth()` using formula 'y ~ x'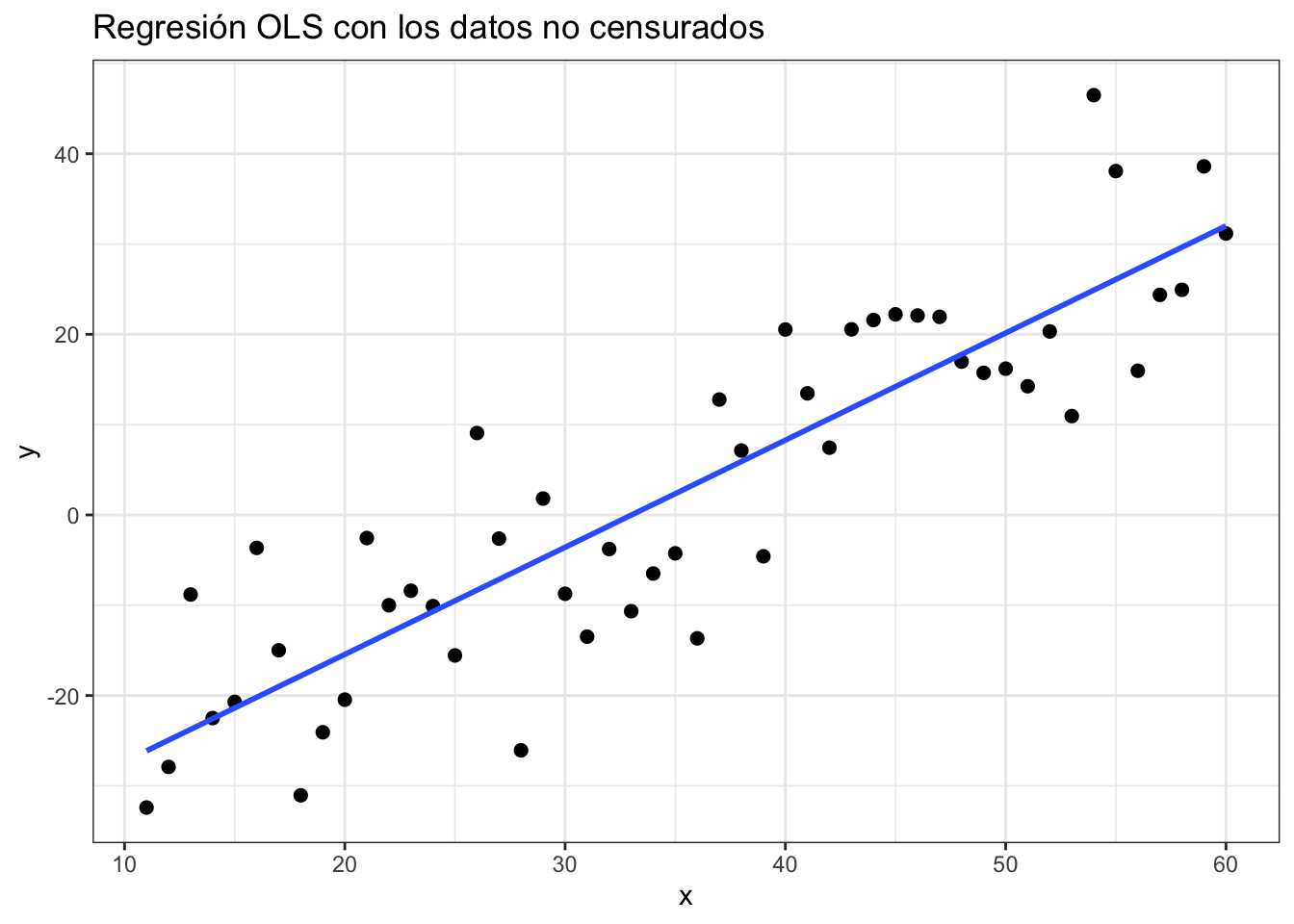

En la gráfica, hemos incluido todas los valores de yi∗y_i^*, incluidos aquellos que son inferiores a cero. Si se cumplen los supuestos de Gauss-Markov sobre el error, la estimación por MCO resultará en estimadores insesgados, eficientes y consistentes.

Supogamos ahora que no se observan todos los valores de yi∗y_i^*. En particular, imaginemos que los valores inferiores a 00 no pueden cuantificarse, aunque se sabe que existen. En este caso, la muestra disponible se vería como sigue:

ggplot(data = db, aes(x = x, y = y)) +
geom_point(size = 2) +
geom_point(data = filter(db, y < 0), size = 2, color = "grey") +
geom_hline(yintercept = 0, linetype = "dashed") +
theme_bw() +
labs(title = "Muestra disponible")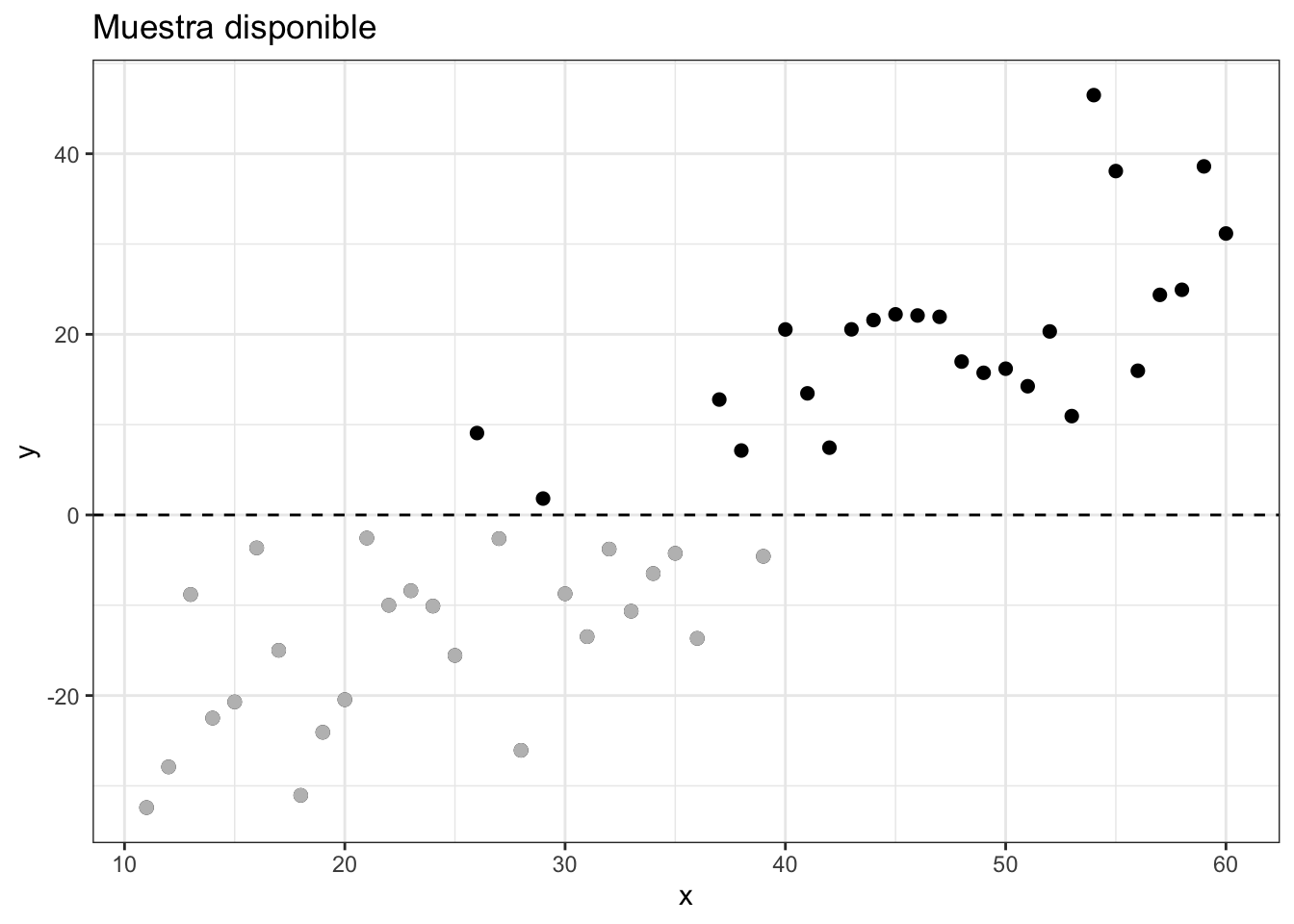

En el caso anterior, una posibilidad que tienen los investigadores es la de recodificar a todos los valores de yi∗y_i^* inferiores a cero (es decir, los valores no observados de yi∗y_i^*) como 00. En este caso, la variable observada yiy_i es exactamente como la definida arriba.Si hacemos esto, ¿cuál sería la consecuencia de estimar el modelo por el método de los MCO?

db_censurada <- db
db_censurada$y[db_censurada$y < 0] <- 0
ggplot(data = db_censurada, aes(x = x, y = y)) +
  geom_point(size = 2) +
  geom_point(data = filter(db_censurada, y == 0),
             size= 2, color = "gray") +
  geom_smooth(data = db,method = "lm", se = FALSE)+
  geom_smooth(data = db_censurada, method = "lm", se=FALSE, color = "red") +
  geom_hline(yintercept = 0, linetype = "dashed") +
  theme_bw() +
  labs(title = "Regresión OLS con los datos censurados")
## `geom_smooth()` using formula 'y ~ x'
## `geom_smooth()` using formula 'y ~ x'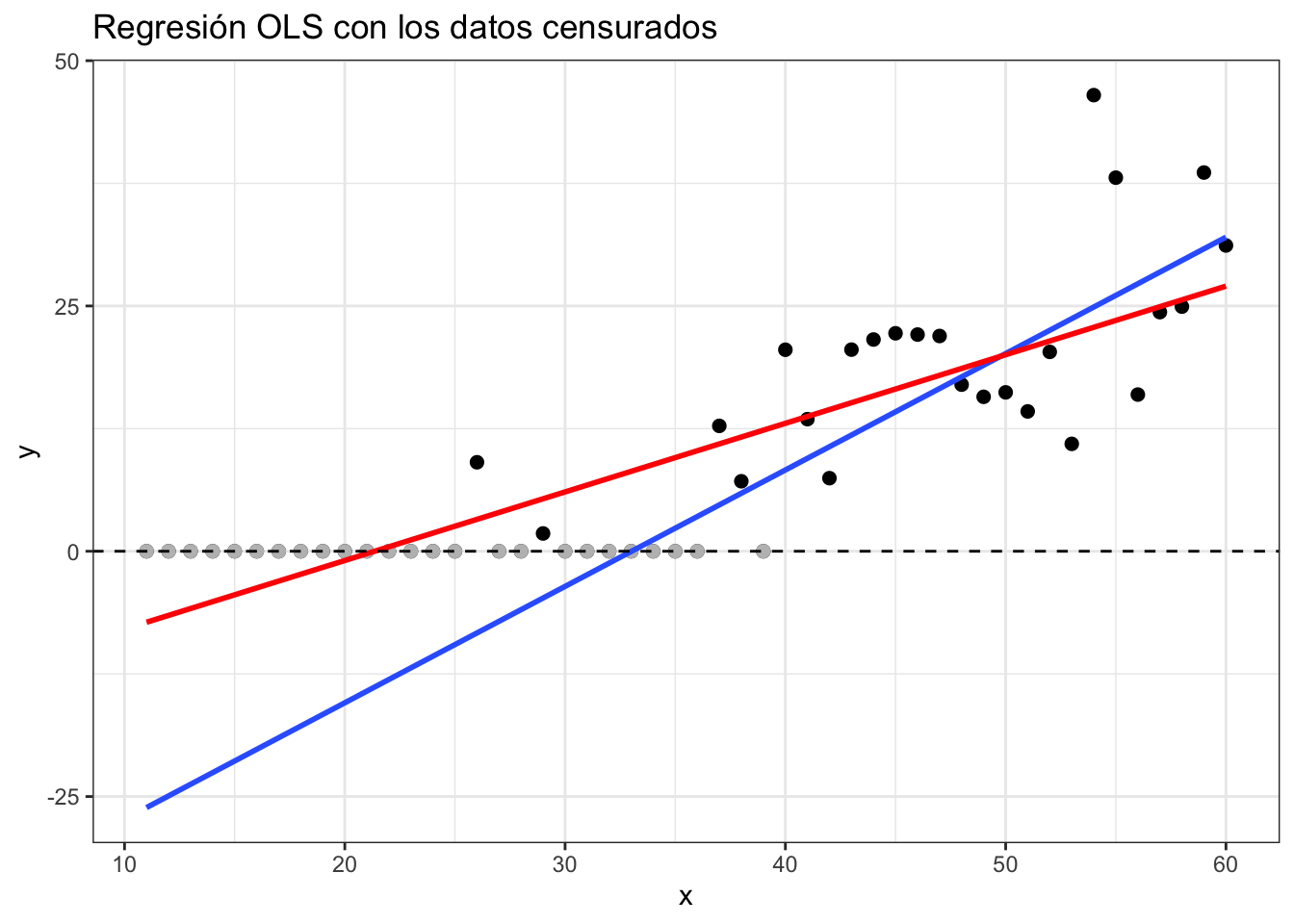

En la gráfica, la línea azul es la línea de regresión verdadera; es decir, aquella en la cual utilizamos todos los valores de yi∗y_i^*. La línea roja es la línea de regresión una vez censurados los datos; es decir, aquella en la cual utilizamos yiy_i en lugar de yi∗y_i^*. Claramente ambas líneas son diferentes (diferente intercepto y diferente pendiente). Esto es un indicativo del sesgo asociado a la estimación por MCO cuando utilizamos datos censurados. Adicionalmente, es claro que, a medida que se aproxima el límite de censura y más observaciones son fijadas al valor establecido, la varianza se reduce, perdiéndose así la condición de homocedasticidad y de independencia.

¿Entonces?

El modelo Tobit: algunos tecnicismos

Nota: el lector no interesado en la parte técnica puede saltarse esta sección

Para poder construir la función de verosimilitud Tobit, definimos primero la función indicatriz:

wi={1 si yi>00 si yi=0w_i = \begin{cases} 1 & \ \text{si} \ y_i>0 \\ 0 & \ \text{si} \ y_i= 0 \\ \end{cases}

En este caso:

f(yi∣x)={f(yi∗∣x) si wi=1P(yi=0∣x) si wi=0,f(y_i|\mathbf{x}) = \begin{cases} f(y^*_i|\mathbf{x}) & \ \text{si} \ w_i=1 \\ \mathbb{P}(y_i=0|\mathbf{x}) & \ \text{si} \ w_i= 0 \\ \end{cases},

o bien:

f(yi∣x)=[f(yi∗∣x)]wi[P(yi=0∣x)]1−wif(y_i|\mathbf{x}) = [f(y^*_i|\mathbf{x})]^{w_i}[\mathbb{P}(y_i=0|\mathbf{x})]^{1-w_i} Bajo el supuesto de normalidad del término de error, tenemos:

f(yi∗∣x)=12πσ2exp⁡[−12σ2(yi∗−xiβ)2]=ϕ(xiβσ)f(y^*_i|\mathbf{x})=\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left[-\frac{1}{2\sigma^2}\left(y_i^*-\mathbf{x}_i\boldsymbol{\beta}\right)^2\right]=\phi\left(\frac{\mathbf{x}_i\boldsymbol{\beta}}{\sigma}\right) Además, si wi=w_i=, la variable latente, yi∗y_i^* debe ser menor o igual que cero:

P(yi=0∣x)=P(yi∗≤0)=P(ui≤−xiβ)=Φ(−xiβσ)1−Φ(xiβσ)\begin{aligned} \mathbb{P}(y_i=0|\mathbf{x}) &=\mathbb{P}(y_i^*\leq 0)=\mathbb{P}(u_i \leq -\mathbf{x}_i\boldsymbol{\beta})=\Phi\left(\frac{-\mathbf{x}_i\boldsymbol{\beta}}{\sigma}\right) \\ &1-\Phi\left(\frac{\mathbf{x}_i\boldsymbol{\beta}}{\sigma}\right)\end{aligned}

Entonces, la contribución a la verosimilitud de una observación cualquiera (censurada o no) es:

f(yi∣xi)=[ϕ(xiβσ)]wi[1−Φ(xiβσ)]1−wi f(y_i|\mathbf{x}_i)=\left[\phi\left(\frac{\mathbf{x}_i\boldsymbol{\beta}}{\sigma}\right)\right]^{w_i}\left[1-\Phi\left(\frac{\mathbf{x}_i\boldsymbol{\beta}}{\sigma}\right)\right]^{1-w_i} Por lo tanto, la función de verosimilitud Tobit es:

L=∏i=1N[ϕ(xiβσ)]wi[1−Φ(xiβσ)]1−wi L=\prod_{i=1}^{N}\left[\phi\left(\frac{\mathbf{x}_i\boldsymbol{\beta}}{\sigma}\right)\right]^{w_i}\left[1-\Phi\left(\frac{\mathbf{x}_i\boldsymbol{\beta}}{\sigma}\right)\right]^{1-w_i} El objetivo es estimar el conjunto de coeficientes en el vector β\boldsymbol{\beta} más un estimador de σ\sigma. Nota que no es necesario estimar el umbral para el cual censuramos la variable yi∗y_i^*, ya que este umbral está determinado por los datos.

El modelo Tobit: ejemplo

En R existen varios paquetes que nos permiten estimar los coeficientes de un modelo Tobit. Aquí utilizaremos el paquete VGAM y. En nuestro ejemplo con datos simulados tenemos:

modelo_tobit <- vglm(y ~ x, tobit(Lower = 0), data = db)
## Warning in eval(slot(family, "initialize")): replacing response values less than
## 'Lower' by 'Lower'
summary(modelo_tobit)
## 
## Call:
## vglm(formula = y ~ x, family = tobit(Lower = 0), data = db)
## 
## Pearson residuals:
##                 Min      1Q  Median       3Q   Max
## mu          -1.5217 -0.5428 -0.1056  0.29831 2.293
## loglink(sd) -0.8366 -0.3247 -0.1517 -0.02119 4.090
## 
## Coefficients: 
##               Estimate Std. Error z value Pr(>|z|)    
## (Intercept):1 -44.3792     7.1206  -6.232 4.59e-10 ***
## (Intercept):2   2.1944     0.1389  15.802  < 2e-16 ***
## x               1.3013     0.1569   8.293  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Names of linear predictors: mu, loglink(sd)
## 
## Log-likelihood: -97.397 on 97 degrees of freedom
## 
## Number of Fisher scoring iterations: 7 
## 
## Warning: Hauck-Donner effect detected in the following estimate(s):
## '(Intercept):1'

En la tabla de arriba tenemos:

  • Los coeficientes estimados, sus errores estándar y el estadístico z (recuerda que hemos supuesto que los errores siguen una distribución normal). No se incluyen los valores p, pero se pueden calcular muy fácilmente. Esto lo haremos más abajo.

  • Los coeficientes se interpretan de la misma forma que los coeficientes de una regresión por MCO. Sin embargo, es importante resaltar que estos miden el efecto de las variables explicativas sobre la variable latente no censurada, yi∗y_i^*. Por ejemplo, un incremento en una unidad de xx incrementa el valor de yi∗y_i^* en 1.30 unidades. (¿Recuerdas que en el proceso generador de datos el coeficiente verdadero es igual 1.2?)

  • El coeficiente etiquetado como “(Intercept):1” es el intercepto estimado del modelo. En nuestro ejemplo este es -44.379. (¿Recuerdas que en el proceso generador de datos el coeficiente verdadero es igual -40?)

  • El coeficiente etiquetado como “(Intercept):2” es un estadístico auxiliar. Si calculamos la exponencial de este valor, obtenemos el análogo de la raiz cuadrada de la varianza de los residuales en una regresión por MCO.

Calculamos ahora los valores p para las pruebas de significancia de los coeficientes estimados:

ctable <- coef(summary(modelo_tobit))
pvals <- 2 * pt(abs(ctable[, "z value"]), df.residual(modelo_tobit), lower.tail = FALSE)
cbind(ctable, pvals)
##                 Estimate Std. Error   z value     Pr(>|z|)        pvals
## (Intercept):1 -44.379202  7.1206426 -6.232472 4.591329e-10 1.188387e-08
## (Intercept):2   2.194396  0.1388683 15.801995 3.014268e-56 1.404421e-28
## x               1.301345  0.1569162  8.293250 1.101956e-16 6.365967e-13

Con esto, podemos ver que los coeficientes del modelo son altamento significativos, puesto que los valores p son inferiores a α=0.1%\alpha=0.1\%.

¿Qué tan conveniente es usar un modelo Tobit?

El modelo Tobit presenta algunos inconvenientes que resultan evidentes de nuestra discusión:

  • El modelo depende crucialmente de los supuestos de normalidad y homoscedasticidad del término de error. De hecho, a diferencia del modelo de regresión lineal (para el cual tenemos estimadores consistentes y se pueden calcular errores estándar robustos), en el modelo Tobit la estimación y la inferencia se invalidan totalmente en presencia de heteroscedasticidad y/o no normalidad.

  • El modelo impone el mismo mecanismo para determinar la probabilidad de censura y el valor de las observaciones no censuradas. En nuestro ejemplo, la variable xix_i determina tanto el valor de yi∗y_i^* como las razones por las que yi∗=0y_i^*=0 o yi∗>0y_i^*>0.

Por estas razones, el modelo Tobit se utiliza muy pocas veces en la práctica.

Última actualización: 02-09-2020.