Modelos en dos partes

Tue, Sep 29, 2020 11-minute read

En muchas ocasiones, la variable dependiente, $y_i$ , puede pensarse como una mezcla de variables aleatorias continuas y discretas. Esto ocurre cuando $y_i \geq 0$ , y, al mismo tiempo, el número de observaciones para las cuales $y_i=0$ es lo suficientemente grande tal que se justifique un trato especial. A este fenómeno se le conoce como el de los datos censurados.

Para hacer frente a un modelo con datos censurados, podemos suponer que la función de densidad de la variable dependiente es una mezcla de dos procesos: 1) el proceso que genera los ceros y 2) el proceso que genera los valores positivos. Sea $f_0$ la densidad de $y_i$ cuando $y_i=0$ y sea $f_+$ la densidad condicional de $y_i$ cuando $y_i>0$ . Entonces, la función de densidad de $y_i$ , la cual llamaremos $g(\cdot)$ , puede escribirse como:

$g(y_i|\mathbf{x}_i)=\begin{cases}[1-\mathbb{P}(y_i>0|\mathbf{x}_i)]\times f_0(0|y_i=0, \mathbf{x}_i) & \text{si} \ y_i=0 \\ \mathbb{P}(y_i>0|\mathbf{x}_i)\times f_+(y_i|y_i>0, \mathbf{x}_i) & \text{si} \ y_i>0 \end{cases}$

donde $f_0(0|y_i=0, \mathbf{x}_i)=1$ , debido a que esta define una densidad degenerada en $y=0$ . Nota que esta definición no implica ninguna relación particular entre $\mathbb{P}(\cdot)$ y $f_+$ (y $f_0$ ). Esto es, no se requiere suponer independencia entre distribuciones.

Cuando la función de densidad de la variable dependiente tiene estas características, podemos descomponer los coeficientes del modelo en dos partes: los parámetros del modelo para $\mathbb{P}(y_i>0|\mathbf{x}_i)$ se estiman de forma separada de los coeficientes del modelo para $f_+(y_i|y_i>0, \mathbf{x}_i)$ . Esta es la razón por la que a este modelo se lo conoce como modelo en dos partes. Por ejemplo, deseamos explicar los gastos hospitalarios de un individuo. En este caso, un modelo en dos partes nos permite explicar en primer lugar el porqué de la hospitalización y, en segundo lugar (y de forma separada), los gastos de este individuo una vez en el hospital.

Lo anterior implica que es necesario hacer una elección sobre el modelo a utilizar en la primera y segunda partes de la estimación. Hay muchas posibles combinaciones, algunas de las cuales se pueden deducir de la siguiente tabla:

Primera parte	Segunda parte
Probit	GLM Gaussiano
Logit	GLM Poisson
	GLM Gamma
	GLM Gaussiana Inversa
	$\ln(y)$
	$\sqrt(y)$
	$y$

Ejemplos de estimación con modelos en dos partes

Para los siguientes ejemplos, estaremos utilizando los siguientes paquetes de R:

# Instalar paquetes si es necesario
# install.packages("tidyverse")

# Leer paquetes
library(tidyverse)

## Warning: package 'tidyverse' was built under R version 4.0.2

## ── Attaching packages ─────────────────────────── tidyverse 1.3.0 ──

## ✓ ggplot2 3.3.2     ✓ purrr   0.3.4
## ✓ tibble  3.0.1     ✓ dplyr   1.0.0
## ✓ tidyr   1.1.0     ✓ stringr 1.4.0
## ✓ readr   1.3.1     ✓ forcats 0.5.0

## ── Conflicts ────────────────────────────── tidyverse_conflicts() ──
## x dplyr::filter() masks stats::filter()
## x dplyr::lag()    masks stats::lag()

Consideremos una muestra del Medical Expenditure Panel Survey 2004 de los Estados Unidos. Tómate un tiempo para analizar la base de datos, así como para realizar un análisis de estadística descriptiva.

db <- read_csv("https://raw.githubusercontent.com/amosino/courses--econometria/master/econometria_salud/econometria_salud--datos/MEPSData.csv")

## Parsed with column specification:
## cols(
##   .default = col_double(),
##   famidyr = col_character(),
##   hieuidx = col_character(),
##   female = col_character(),
##   race_bl = col_character(),
##   race_oth = col_character(),
##   eth_hisp = col_character(),
##   ed_hs = col_character(),
##   ed_hsplus = col_character(),
##   ed_col = col_character(),
##   reg_midw = col_character(),
##   reg_south = col_character(),
##   reg_west = col_character(),
##   anylim = col_character(),
##   ins_mcare = col_character(),
##   ins_mcaid = col_character(),
##   ins_unins = col_character(),
##   ins_dent = col_character()
## )

## See spec(...) for full column specifications.

Deseamos modelar la dependencia que existe entre los gastos totales en salud (exp_tot), los cuales juegan el papel de la variable dependiente, en función de la edad de la persona (age) y de su género (female). Esta es una variable dummy que vale Female si la observación es una mujer y Malesi es hombre. Aunque R no tiene ningún problema manejando variables dummy cuyas características estén codificadas como texto, podemos recodificar, si así lo deseamos, la variable female, tal que esta valga 1 si la observación es una mujer y 0 si es hombre.

db$female <- as.factor(as.numeric(db$female=="Female"))

Un histograma de la variable dependiente revela que esta está muy sesgada hacia la izquierda, lo que indica que el método de los mínimos cuadrados ordinarios podría no ser el mejor método de estimación.

hist(db$exp_tot)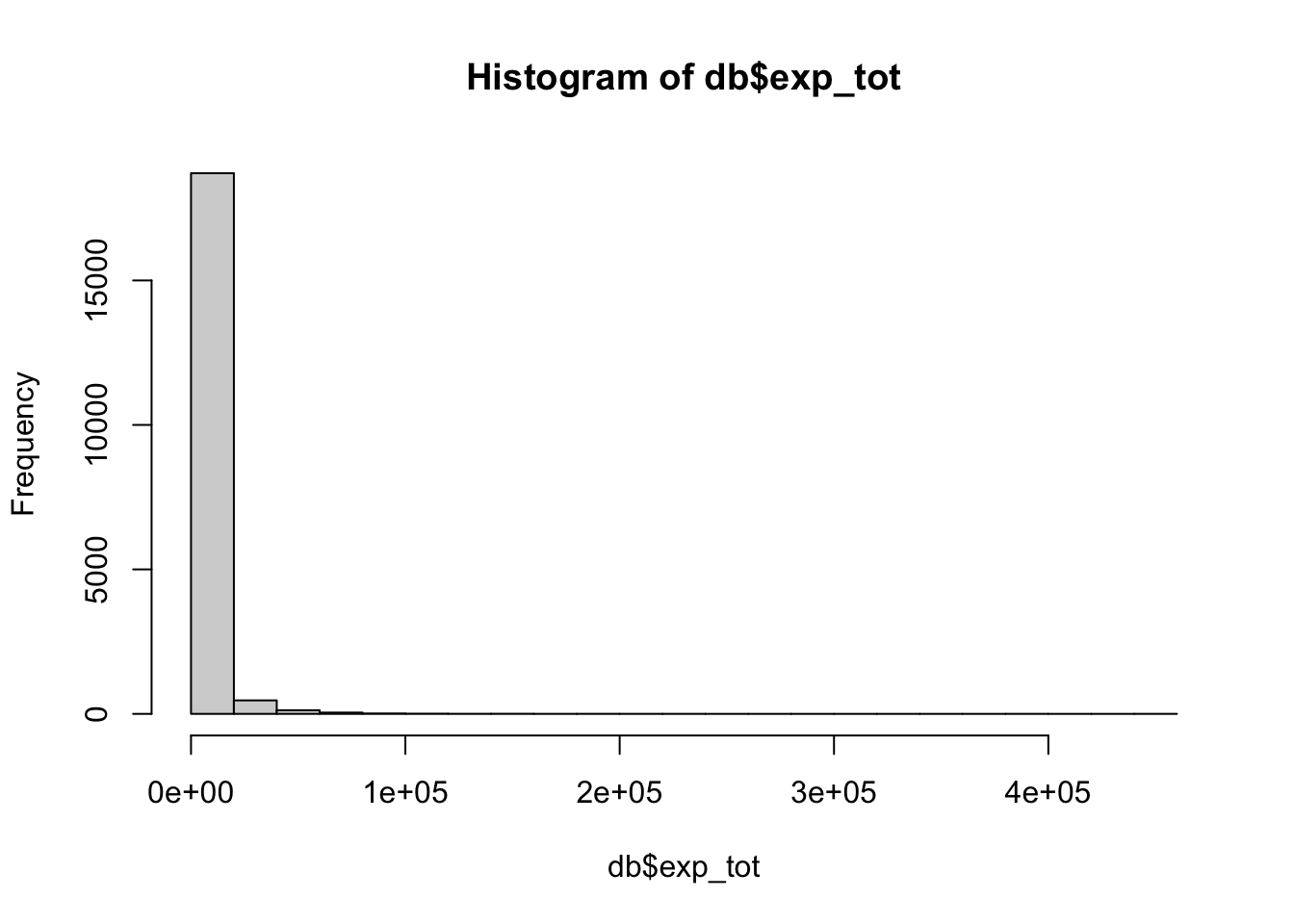

De hecho, podemos correr una regresión por el método de los MCO y recuperar sus residuales. ¿Te parece que estos cumplen con los supuestos de Gauss-Markov?

mod.lrm <- lm(exp_tot~age+female, data=db, subset=(exp_tot>0))
smod.lrm <- summary(mod.lrm)
print(smod.lrm)

## 
## Call:
## lm(formula = exp_tot ~ age + female, data = db, subset = (exp_tot > 
##     0))
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
##  -9422  -3676  -1968     62 438341 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -1819.043    256.984  -7.078 1.52e-12 ***
## age           125.064      4.669  26.787  < 2e-16 ***
## female1       624.556    167.018   3.739 0.000185 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 10370 on 15943 degrees of freedom
## Multiple R-squared:  0.04373,    Adjusted R-squared:  0.04361 
## F-statistic: 364.5 on 2 and 15943 DF,  p-value: < 2.2e-16

res2 <- residuals(mod.lrm)^2
hist(res2)

Ahora, consideremos la estimación de los coeficientes considerando un modelo en dos partes.

Como primer paso, creamos una variable dummy para la variable dependiente, $exp_tot$ . Esta tendrá un valor de 0 cuando $exp_tot=0$ y de 1 cuando $exp_tot>0$ .

db$d_exp_tot <- as.factor(as.numeric(db$exp_tot>0))

Esta nueva variable nos permite estimar la primera parte del modelo. En este ejemplo utilizaremos un modelo tipo probit.

probit.fit <- glm(d_exp_tot~age+female, data=db,
                  family = binomial(link="probit"))
summary(probit.fit)

## 
## Call:
## glm(formula = d_exp_tot ~ age + female, family = binomial(link = "probit"), 
##     data = db)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -3.0455   0.2367   0.4689   0.6844   1.1509  
## 
## Coefficients:
##               Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -0.4348369  0.0339372  -12.81   <2e-16 ***
## age          0.0263418  0.0007494   35.15   <2e-16 ***
## female1      0.5342665  0.0225372   23.71   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 18126  on 19385  degrees of freedom
## Residual deviance: 16118  on 19383  degrees of freedom
## AIC: 16124
## 
## Number of Fisher Scoring iterations: 5

Los resultados de la estimación nos indican, por ejemplo, que la probabilidad de realizar algún gasto en salud (sin importar el monto) se incrementa con la edad. Además, la probabilidad de realizar gastos en salud es mayor para las mujeres que para los hombres. Para calcular los valores exactos hacemos uso de la función predict(). Por ejemplo, las siguiente líneas de código nos permiten estimar la probabilidad de realizar gastos en salud para una mujer de 60 años. Como vemos, la probabilidad estimada es de 95%.

dbex <-  data.frame(age=60, female="1")
predict(probit.fit, newdata=dbex, type="response", se.fit=TRUE)

## $fit
##         1 
## 0.9535154 
## 
## $se.fit
##           1 
## 0.002249526 
## 
## $residual.scale
## [1] 1

Ahora estamos listos para estimar la segunda parte del modelo. Utilizaremos dos diferentes estimaciones: modelo con conexión logaritmica y distribución gamma y modelo con conexión lineal y distribución gaussiana (es decir, un modelo de regresión lineal). Naturalmente, para la estimación solo tomamos en cuenta las observaciones para las cuales $exp_tot>0$ .

Primero el modelo con conexión lineal y distribución gamma.

gamma.fit <- glm(exp_tot~age+female,
                 data=db, subset=(exp_tot>0),
                 family=Gamma(link=log))
summary(gamma.fit)

## 
## Call:
## glm(formula = exp_tot ~ age + female, family = Gamma(link = log), 
##     data = db, subset = (exp_tot > 0))
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -3.5466  -1.5229  -0.8463  -0.0129  19.3542  
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 6.835698   0.066017 103.544  < 2e-16 ***
## age         0.027951   0.001199  23.305  < 2e-16 ***
## female1     0.208600   0.042906   4.862 1.17e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for Gamma family taken to be 7.097201)
## 
##     Null deviance: 37405  on 15945  degrees of freedom
## Residual deviance: 33478  on 15943  degrees of freedom
## AIC: 292919
## 
## Number of Fisher Scoring iterations: 8

Los resultados indican que cada año adicional de vida incrementa la cantidad de gastos médicos en 2.79% en promedio. Así mismo, las mujeres gastan en servicios médicos 23% más que los hombres [0.23 = exp(0.208)-1]. Ambas variables son significativas con un nivel de significancia del 1%.

Ahora estimamos un modelo con conexión lineal y distribución gaussiana.

ols.fit <- glm(exp_tot~age+female,
               data=db, subset=(exp_tot>0))
summary(ols.fit)

## 
## Call:
## glm(formula = exp_tot ~ age + female, data = db, subset = (exp_tot > 
##     0))
## 
## Deviance Residuals: 
##    Min      1Q  Median      3Q     Max  
##  -9422   -3676   -1968      62  438341  
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -1819.043    256.984  -7.078 1.52e-12 ***
## age           125.064      4.669  26.787  < 2e-16 ***
## female1       624.556    167.018   3.739 0.000185 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for gaussian family taken to be 107543722)
## 
##     Null deviance: 1.7930e+12  on 15945  degrees of freedom
## Residual deviance: 1.7146e+12  on 15943  degrees of freedom
## AIC: 340154
## 
## Number of Fisher Scoring iterations: 2

Ambas variables aun son significativas al 1%, aunque la lectura de los coeficientes estimados es diferente. En este caso tenemos que los gastos médicos se incrementan (en promedio) en 125.06 dólares con cada año adicional de vida. Además, las mujeres gastan (en promedio) 624.5 dólares más que los hombres.

Una de las bondades de utilizar modelos lineales generalizados es que los resultados anteriores son directamente comparables. Para esto, podemos utilizar los criterios de información de Akaike (AIC) y Schwartz (BIC).

AIC.m1 <- AIC(gamma.fit, k=2)
BIC.m1 <- BIC(gamma.fit)
AIC.m2 <- AIC(ols.fit, k=2)
BIC.m2 <- BIC(ols.fit)
l.AIC <- c(AIC.m1, AIC.m2)
l.BIC <- c(BIC.m1, BIC.m2)
IC <- data.frame("AIC" = l.AIC, "BIC" = l.BIC)
print(IC)

##        AIC      BIC
## 1 292919.2 292949.9
## 2 340153.7 340184.4

Claramente, el mejor modelo es el de conexión logaritmica y distribución gamma. Esto debido a que tiene los valores de AIC y BIC más bajos.

Nota que en la estimación de la primera y segunda partes del modelo hemos utilizado las mismas variables explicativas. Sin embargo, dado que se trata de modelos independientes esto no tiene porqué ser así.

Ahora bien, ¿cómo podemos hacer predicciones utilizando las dos partes del modelo? Para esto, recordemos que la función $g(\cdot)$ depende de $\mathbb{P}(y_i>0|\mathbf{x}_i)$ , la cual se obtiene de la estimación en la primera parte, y de $f_+(y_i|y_i>0, \mathbf{x}_i)$ , la cual se obtiene de la estimación en la segunda parte. Desde un punto de vista práctico, para pronosticar los gastos en salud de una persona que ya se encuentra en el hospital necesitamos multiplicar las probabilidades estimadas por el modelo probit por los valores de $y$ predichos por el modelo lineal generalizado.

Si en la primera parte usamos un modelo probit y en la segunda parte usamos una distribución gamma con conexión logaritmica tenemos:

# Pronóstico primera parte
fp <- predict(probit.fit, db, type = "response")
# Pronóstico seguda parte
sp_gamma <- predict(gamma.fit, db, type = "response")
# Tabla
probs.table <- data.frame(exp_tot = db$exp_tot)
probs.table$gamma <- fp*sp_gamma
print(head(probs.table))

##   exp_tot    gamma
## 1      80 2942.840
## 2     145 3512.980
## 3    7485 1857.790
## 4       0 1922.679
## 5    4154 1929.093
## 6    8591 3753.140

Nota que en las últimas líneas del código hemos construido una tabla que en su primer columna contiene los valores verdaderos de $exp_tot$ y en la segunda los valores pronosticados por el modelo en dos partes. Al menos para las observaciones que se muestran, parece que el pronóstico no es muy bueno. Esto no es tan extraño tomando en cuenta lo limitado (en cuestión de la elección de las variables explicativas) de nuestro modelo.

Hacemos el mismo ejercicio utilizando en la primera parte un modelo probit y en la segunda un modelo de regresión lineal clásico. Naturalmente, la primera parte en este ejemplo es idéntica a la primera parte del ejercicio anterior, por lo que no incluimos esta en el siguiente bloque de código:

# Pronóstico seguda parte
sp_ols <- predict(ols.fit, db, type = "response")
# Tabla
probs.table$ols <- fp*sp_ols
print(head(probs.table))

##   exp_tot    gamma      ols
## 1      80 2942.840 3464.417
## 2     145 3512.980 3859.791
## 3    7485 1857.790 1611.951
## 4       0 1922.679 2095.485
## 5    4154 1929.093 1726.634
## 6    8591 3753.140 4125.852

Como puede verse en la tabla, ninguno de los dos modelos parece hacerlo demasiado bien. Sin embargo, sí podemos saber qué modelo lo hace mejor. Para esto calcularemos la raiz cuadrada del error cuadrático medio (RMSE):

RMSE <- function(x, y)  sqrt(mean((y - x)^2, na.rm = TRUE))
rmse <- c(RMSE(probs.table$exp_tot, probs.table$gamma),
          RMSE(probs.table$exp_tot, probs.table$ols))
names(rmse) <- c("Gamma", "OLS")
print(rmse)

##    Gamma      OLS 
## 9490.948 9486.684

Nota que ambos modelos tienen un error de predicción similar. De hecho, el modelo cuya segunda parte es un modelo de regresión lineal ajusta un poco mejor a los datos verdaderos (es decir, tiene un valor de RMSE más pequeño). Esto a pesar de que los errores del modelo parecen no seguir una distribución normal.

Última actualización: 01-10-2020.

Econometría & Co.

Modelos en dos partes

Ejemplos de estimación con modelos en dos partes